Eine natürliche Zahl, die identisch ist mit ihrer Kehrzahl wie z.B. 131, wird Palindrom genannt. In dieser Fallstudie betrachten wir eine nicht deterministische Methode zur Berechnung beliebig großer Palindrome.
Die in C++ eingebauten elementaren Datentypen (wie int oder long) stellen keine echte Hilfe dar,
wenn wir potentiell unendlich große Palindrome berechnen wollen.
Zu diesem Zweck entwerfen wir im Folgenden zunächst eine Klasse Number, mit deren Hilfe sich
sehr große Zahlen darstellen lassen. Im Anschluss daran gehen wir auf die Klasse PalindromCalculator ein,
um Palindrome zu berechnen.
Lernziele
- Container
std::vector<int> - Klasse
std::string_view - Utility-Klassen
std::tupleundstd::optional - Konstrukt
if constexpr - Einsatz von
std::reverse_iterator - Verschiebesemantik mit
std::move - STL-Algorithmen bzw. -Funktionen
std::for_each,std::find_if,std::begin,std::end,std::rbegin,std::rend,std::isdigitundstd::remove
Aufgabe
Für die Erzeugung von Palindromen gibt es einen sehr einfachen Algorithmus, der leider nicht immer funktioniert: Man addiere eine beliebige Zahl mit ihrer Kehrzahl und untersuche das Ergebnis daraufhin, ob man eine Spiegelzahl erhalten hat. Wenn nicht, setze man das Spiel fort, bis das Ergebnis ein Palindrom ist, zum Beispiel:
165 + 561 ⇒ 726 + 627 ⇒ 1353 + 3531 = 4884
Da dieser Algorithmus nicht immer funktioniert, muss man darauf achten, dass man nicht in eine Endlosschleife gerät!
Zur Lösung der Aufgabe sind zwei Klassen Number und PalindromCalculator zu entwickeln,
deren Arbeitsweise im Folgenden näher beschrieben wird.
Klasse Number
Objekte der Klasse Number beschreiben eine beliebig große Zahl, deren Ziffern durch ein std::string_view-Objekt festgelegt werden.
Im Gegensatz zur Klasse BigInteger aus der Fallstudie
Exakte Arithmetik ganzer Zahlen
sollen Number-Objekte nicht den kompletten Satz
arithmetischer Operationen unterstützen. Es genügt einzig und allein die Addition von Number-Objekten,
um ein nicht-deterministisches Verfahren zur Berechnung von Palindromen implementieren zu können.
Die in Tabelle 1 beschriebenen Elemente der Klasse Number dienen hierzu zur Vorbereitung:
| Element | Beschreibung |
|---|---|
| Konstruktor | Number();Erzeugt ein Number-Objekt zur Zahl 0. |
| Benutzerdefinierter Konstruktor | explicit Number(std::string_view);Erzeugt ein Number-Objekt mit Hilfe der Beschreibung einer Zahl in Form einer Zeichenkette. |
getter size() |
size_t size() const;Liefert die Anzahl der Ziffern der Zahl, auch Stelligkeit der ganzen Zahl genannt, zurück. |
getter symmetric() |
bool symmetric() const;Liefert true zurück, wenn das aktuelle Number-Objekt eine Spiegelzahl ist, andernfalls false. |
Methode add |
Number add(const Number&) const;Addiert zwei beliebig lange Number-Objekte. Das Ergebnis wird als Rückgabewert von add zurückgegeben. |
Methode reverse |
Number reverse() const;Erstellt zum aktuellen Number-Objekt das inverse Number-Objekt, auch als Kehrzahl bezeichnet. Das aktuelle Number-Objekt bleibt unverändert. |
Tabelle 1: Elemente der Klasse Number.
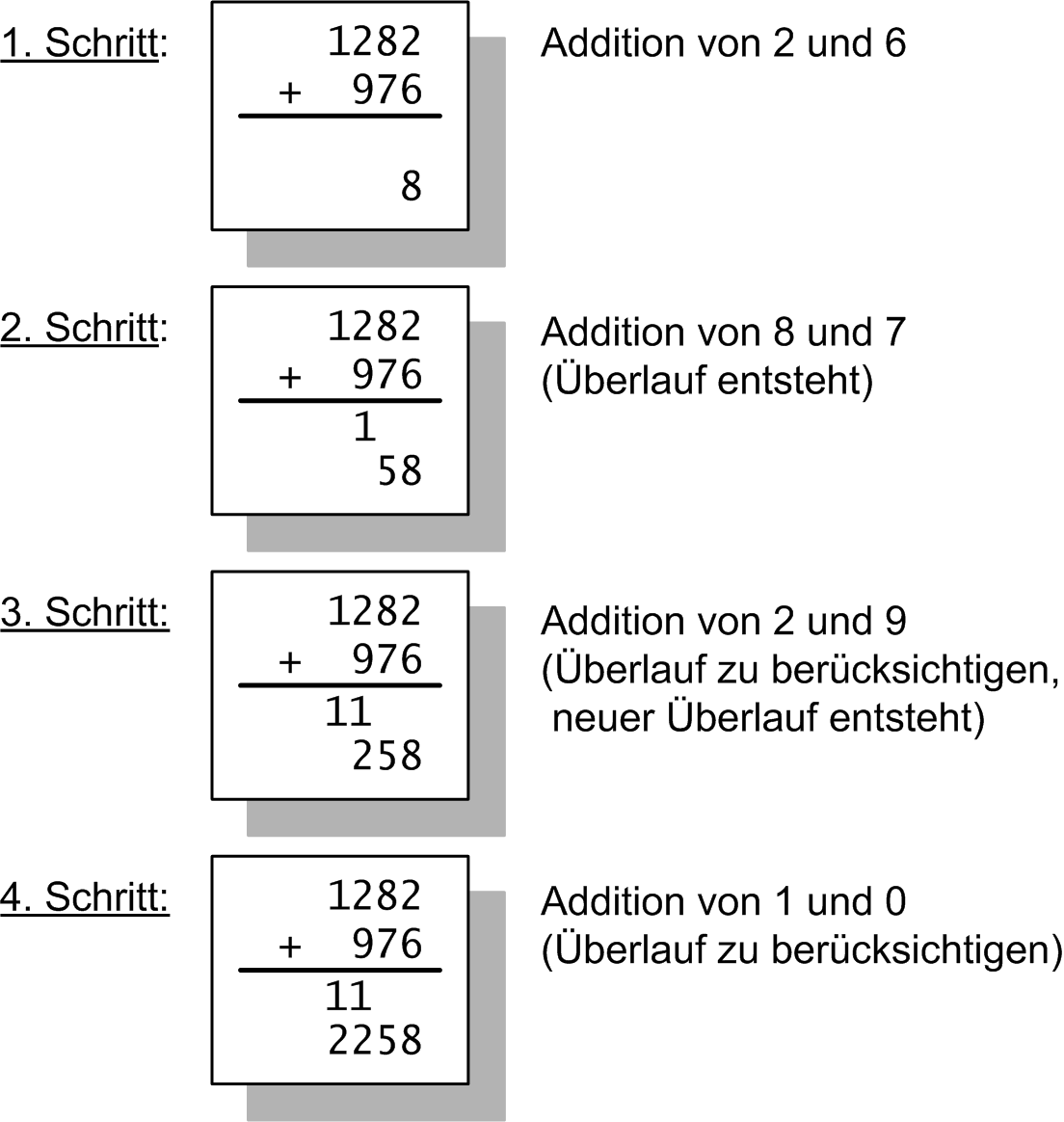
Bei der Additionsmethode add legen Sie Ihre Kenntnisse aus der Schulmathematik zu Grunde:
Die zu addierenden Zahlen sind „gedanklich” betrachtet untereinander zu schreiben.
Die Zahlen werden nun von hinten beginnend aufaddiert, wobei ein Übertrag entstehen kann.
Dieser ist dann im nächsten Schritt zu berücksichtigen, wie in Abbildung 1 am Beispiel
der beiden Zahlen 1282 und 976 dargestellt wird:
Abbildung 1: Schriftliche Addition aus der Schulmathematik.
Anmerkung:
Überlegen Sie sich, in welcher Reihenfolge Sie die Ziffern einer natürlichen Zahl in einem Number-Objekt abspeichern.
Bei geeigneter Ablage kann sich die Implementierung der add-Methode vereinfachen!
Es folgen einige Beispiele, um die Arbeitsweise der Klasse Number näher zu illustrieren:
Beispiel:
Number n{ "1234321" };
std::cout << std::boolalpha << n.symmetric() << std::endl;
Ausgabe:
true
Beispiel:
Number n{ "12345" };
Number m{ n.reverse() };
std::cout << n << std::endl;
std::cout << m << std::endl;
Ausgabe:
12.345
54.321
Beispiel:
Number n1{ "1282" };
std::cout << n1 << std::endl;
Number n2{ "976" };
std::cout << "+ " << n2 << std::endl;
Number n3{ n1.add(n2) };
std::cout << n3 << std::endl;
Ausgabe:
1.282
+ 976
2.258
Klasse PalindromCalculator
Für die Erzeugung von Palindromen gibt es einen Algorithmus, der leider nicht deterministisch ist: Addiert man eine beliebige Zahl wiederholt mit ihrer Kehrzahl (inversen Zahl), kann man ein Palindrom erhalten.
Beispiel:
Zahl: 53978
inverse Zahl: + 87935
addiert: 141913
inverse Zahl: + 319141
addiert: 461054
inverse Zahl: + 450164
addiert: 911218
inverse Zahl: + 812119
addiert: 1723337
inverse Zahl: + 7333271
addiert: 9056608
inverse Zahl: + 8066509
addiert: 17123117
inverse Zahl: + 71132171
addiert: 88255288 7 Schritte
Die einfache Idee des Algorithmus basiert also auf der wiederholten Addition einer beliebigen Zahl mit ihrer inversen Zahl. Da in einigen (wenigen) Situationen der Algorithmus in eine Endlosschleife geraten kann, müssen Sie die Anzahl der wiederholten Additionen begrenzen. Weitere Details entnehmen Sie Tabelle 2:
| Element | Beschreibung |
|---|---|
Methode calcPalindrom |
static std::tuple<std::optional<Number>, Number, size_t> calcPalindrom(const Number& number, size_t steps);.Die Methode versucht, zu einem vorgegebenen Ausgangswert number ein Palindrom zu berechnen. Wird ein Palindrom ermittelt, bricht der Algorithmus ab. Andernfalls erfolgt die Terminierung nach einer festgelegten Anzahl steps von Iterationsschritten. |
Tabelle 1: Elemente der Klasse PalindromCalculator.
Die Methode calcPalindrom liefert ein std::tuple<>-Objekt mit drei Werten zurück:
Dem berechneten Palindrom, falls eines gefunden wurde, dem Ausgangswert der Berechnung und der Anzahl der Iterationsschritte:
std::tuple<std::optional<Number>, Number, size_t>
Für den Umstand, dass ein Palindrom berechnet werden kann oder nicht,
bietet sich die Utility-Klasse std::optional<T> an:
Ein std::optional<T>-Objekt ist ein Hüllenobjekt zu einem anderen Objekt beliebigen Typs T,
in unserem Fall Number: Konnte ein Palindrom und damit ein Number-Objekt berechnet werden,
ist dieses im std::optional<>-Objekt enthalten und via value() verfügbar.
Findet die Berechnung kein Palindrom, liefert die Methode has_value() am Hüllenobjekt
den Wert false zurück.
Im Hüllenobjekt selbst ist dann an Stelle eines Number-Objekts der Wert std::nullopt_t abgelegt.
Damit betrachten wir ein erstes Beispiel:
Beispiel:
Number start{ "89" };
size_t count{ 100 };
const auto& [palindrom, begin, steps] {
PalindromCalculator::calcPalindrom(start, count)
};
std::cout
<< "Searching palindrom beginning at " << begin
<< " [" << steps << " steps]:" << std::endl;
if (palindrom.has_value()) {
std::cout << "Found palindrom: " << palindrom.value() << std::endl;
}
else {
std::cout << "No palindrom found!" << std::endl;
}
Ausgabe:
Searching palindrom beginning at 89 [24 steps]:
Found palindrom: 8.813.200.023.188
Würden wir beim Aufruf von calcPalindrom den Wert des zweiten Parameters mit 20 vorbelegen,
erhalten wir die Ausgabe
Searching palindrom beginning at 89 [20 steps]:
No palindrom found!
Ohne Verwendung von auto müssten wir das letzte Beispiel so formulieren:
Number start{ "89" };
size_t count{ 100 }; // choose 100 for success
std::tuple<std::optional<Number>, Number, size_t> result{
PalindromCalculator::calcPalindrom(start, count)
};
std::cout
<< "Searching palindrom beginning at " << std::get<1>(result)
<< " [" << std::get<2>(result) << " steps]:" << std::endl;
if (std::get<0>(result).has_value()) {
std::cout << "Found palindrom: " << std::get<0>(result).value() << std::endl;
}
else {
std::cout << "No palindrom found!" << std::endl;
}
Natürlich möchte man den Verlauf des Algorithmus auch verfolgen können.
In diesem Fall könnte man mit wenigen Ergänzungen in der Methode calcPalindrom folgende
ausführlicheren Ausgaben erhalten:
Number: 89
Inverse: 98
Number: 187
Inverse: 781
Number: 968
Inverse: 869
Number: 1.837
Inverse: 7.381
Number: 9.218
Inverse: 8.129
Number: 17.347
Inverse: 74.371
Number: 91.718
Inverse: 81.719
Number: 173.437
Inverse: 734.371
Number: 907.808
Inverse: 808.709
Number: 1.716.517
Inverse: 7.156.171
Number: 8.872.688
Inverse: 8.862.788
Number: 17.735.476
Inverse: 67.453.771
Number: 85.189.247
Inverse: 74.298.158
Number: 159.487.405
Inverse: 504.784.951
Number: 664.272.356
Inverse: 653.272.466
Number: 1.317.544.822
Inverse: 2.284.457.131
Number: 3.602.001.953
Inverse: 3.591.002.063
Number: 7.193.004.016
Inverse: 6.104.003.917
Number: 13.297.007.933
Inverse: 33.970.079.231
Number: 47.267.087.164
Inverse: 46.178.076.274
Number: 93.445.163.438
Inverse: 83.436.154.439
Number: 176.881.317.877
Inverse: 778.713.188.671
Number: 955.594.506.548
Inverse: 845.605.495.559
Number: 1.801.200.002.107
Inverse: 7.012.000.021.081
Number: 8.813.200.023.188
Searching palindrom beginning at 89 [24 steps]:
Found palindrom: 8.813.200.023.188
Viertes Eulersches Problem
Ein nach dem Mathematiker Leonhard Euler benanntes Problem lautet: „Finde das größte Palindrom, das ein Produkt aus zwei dreistelligen Zahlen ist!”. Zum besseren Verständnis: Das größte 4-stellige Palindrom als Produkt zweier 2-stelliger Zahlen ist 9009 = 91 * 99.
Hinweis: Für die Multiplikation dreistelliger Zahlen dürfen Sie Variablen des Typs int verwenden.
Sie müssen die Klasse Number also nicht um eine Multiplikationsmethode ergänzen.
Schreiben Sie eine C++-Funktion, die mit Hilfe der Klasse Number das vierte Eulersche Problem löst.
Lösung
Quellcode: Siehe auch Github.
Wir beginnen in Listing 1 und Listing 2 mit der Klasse Number,
die die Basis des nachfolgenden Algorithmus darstellt:
01: class Number
02: {
03: private:
04: std::vector<int> m_digits;
05:
06: public:
07: // c'tors / d'tor
08: Number();
09: explicit Number(std::string_view);
10:
11: // getter
12: size_t size() const;
13: bool symmetric() const;
14:
15: // public interface
16: Number add(const Number&) const;
17: Number reverse() const;
18:
19: private:
20: // private helper methods
21: void removeLeadingZeros();
22:
23: // output
24: friend std::ostream& operator<< (std::ostream&, const Number&);
25: };
Listing 1: Klasse Number: Definition.
Die Realisierung der Klasse Number schließt sich in Listing 2 an:
001: // c'tors / d'tor
002: Number::Number() : m_digits{ 1 } {
003: m_digits[0] = 0;
004: }
005:
006: Number::Number(std::string_view sv)
007: {
008: std::reverse_iterator<std::string_view::iterator> r = sv.rbegin();
009:
010: std::for_each(std::rbegin(sv), std::rend(sv), [this](char ch) {
011: if (ch == '.') {
012: return;
013: }
014: else if (!std::isdigit(ch)) {
015: throw std::invalid_argument("illegal digit in number");
016: }
017: else {
018: m_digits.push_back(ch - '0');
019: }
020: });
021: }
022:
023: // getter
024: size_t Number::size() const
025: {
026: return m_digits.size();
027: }
028:
029: bool Number::symmetric() const
030: {
031: for (int i = 0; i < m_digits.size() / 2; i++) {
032: if (m_digits[i] != m_digits[m_digits.size() - 1 - i])
033: return false;
034: }
035:
036: return true;
037: }
038:
039: // public interface
040: Number Number::add (const Number& number) const
041: {
042: // maximum of number of digits
043: size_t count{ size() >= number.size() ?
044: size() + 1 :
045: number.size() + 1
046: };
047:
048: // add numbers digit per digit
049: std::vector<int> digits;
050: int carry{};
051: for (size_t i{}; i != count; i++)
052: {
053: if (i < size())
054: carry += m_digits[i];
055: if (i < number.size())
056: carry += number.m_digits[i];
057:
058: digits.push_back(carry % 10);
059: carry /= 10;
060: }
061:
062: // move result vector into a 'Number' object
063: Number tmp{};
064: tmp.m_digits = std::move(digits);
065: tmp.removeLeadingZeros();
066: return tmp;
067: }
068:
069: Number Number::reverse() const
070: {
071: std::vector<int> digits{ m_digits };
072: std::reverse(std::begin(digits), std::end(digits));
073:
074: // move digits vector into a 'Number' object
075: Number tmp{};
076: tmp.m_digits = std::move(digits);
077: tmp.removeLeadingZeros();
078: return tmp;
079: }
080:
081: // private helper methods
082: void Number::removeLeadingZeros()
083: {
084: // remove trailing zeros, if any ... using STL algorithms
085: std::reverse_iterator<std::vector<int>::iterator> r_it{ std::find_if(
086: std::rbegin(m_digits),
087: std::rend(m_digits),
088: [](int value) { return value != 0; }
089: ) };
090:
091: m_digits.erase(r_it.base(), std::end(m_digits));
092: }
093:
094: // output
095: std::ostream& operator<< (std::ostream& os, const Number& n)
096: {
097: std::for_each(
098: std::rbegin(n.m_digits),
099: std::rend(n.m_digits),
100: [&, i = n.m_digits.size() - 1](int digit) mutable {
101: os << (char)(digit + '0');
102: if (i > 0 && i % 3 == 0)
103: os << '.';
104: --i;
105: });
106:
107: return os;
108: }
Listing 2: Klasse Number: Realisierung.
Beachten Sie die Zeilen 64 und 76 von Listing 2:
Die Berechnung des Resultats der Addition erfolgte in einem std::vector<int> Objekt.
Als Rückgabewert der Addition benötigen wir aber ein Number Objekt!
In jedem Fall wollen wir vermeiden, dass es bei der Konstruktion dieses Objekts zu einer – unnötigen –
Kopie des beteiligten std::vector<int>-Objekts kommt. Die Verschiebesemantik ist hierzu angesagt.
In Zeile 64 bzw. 76 verschieben wir das Resultat-Vektorobjekt mittels des Verschiebewertzuweisungsoperators,
der von der Klasse std::vector<> bereitgestellt wird, in das Number-Objekt.
Dazu wandeln wir die LValue-Referenz des Arguments digits mit Hilfe von std::move in eine RValue-Referenz um!
Die Implementierung eines nicht-deterministischen Algorithmus zum Berechnen von Palindromen stellen wir
an Hand der Klasse PalindromCalculator in Listing 3 und Listing 4 vor.
Die Klasse besteht nur aus zwei Klassenmethoden, eine zum Berechnen von Palindromen und eine zweite,
um das vierte Eulersche Problem zu lösen:
01: class PalindromCalculator
02: {
03: public:
04: PalindromCalculator() = delete;
05:
06: static std::tuple<std::optional<Number>, Number, size_t>
07: calcPalindrom(const Number&, size_t);
08:
09: static std::tuple<size_t, size_t, size_t> forthEulerProblem();
10: };
Ein Hinweis zu Zeile 4 von Listing 3: Da wir von der Klasse PalindromCalculator keine Objekte anlegen wollen,
fügen wir in die Klassendeklaration einen Hinweis ein (Schlüsselwort delete in Zeile 4)`, der zum Ausdruck bringt,
dass der Standardkonstruktor dieser Klasse nicht zur Verfügung steht.
Listing 3: Klasse PalindromCalculator: Definition.
01: constexpr bool Verbose = true;
02:
03: std::tuple<std::optional<Number>, Number, size_t>
04: PalindromCalculator::calcPalindrom(const Number& start, size_t steps)
05: {
06: Number n{ start };
07: for (size_t i{}; i != steps; i++) {
08:
09: if constexpr (Verbose) {
10: std::cout << "Number: " << n << std::endl;
11: }
12:
13: if (n.symmetric()) {
14: return { n, start, i };
15: }
16:
17: Number m{ n.reverse() };
18: n = n.add(m);
19:
20: if constexpr (Verbose) {
21: std::cout << "Inverse: " << m << std::endl;
22: }
23: }
24:
25: return { std::nullopt, start, steps };
26: }
27:
28: std::tuple<size_t, size_t, size_t>
29: PalindromCalculator::forthEulerProblem()
30: {
31: size_t i{ 1 }, j{ 1 };
32: size_t candidate{ 1 };
33:
34: for (size_t n{ 111 }; n != 999; ++n)
35: {
36: for (size_t m{ 111 }; m != 999; ++m)
37: {
38: if (n < m)
39: {
40: size_t prod{ n * m };
41: std::string s{ std::to_string(prod) };
42: Number num{ s };
43:
44: if (num.symmetric() and prod > candidate)
45: {
46: i = n;
47: j = m;
48: candidate = i * j;
49: }
50: }
51: }
52: }
53:
54: return { candidate, i, j };
55: }
Listing 4: Klasse PalindromCalculator: Realisierung.
Leider produziert die calcPalindrom-Methode nicht bei jedem ihrer Aufrufe ein Palindrom.
Wir müssen aus diesem Grund die Klasse PalindromCalculator sehr sorgfältigen Tests unterziehen – einen Ausschnitt des Testszenarios
finden Sie in den nachfolgenden Ausschnitten vor. Eine interessante Website zum Thema
„Reversal-Addition Palindrome Records” findet man unter What is a Palindrome?.
Eine Kostprobe gefällig? Die Zahl 1.186.060.307.891.929.990 wird dort getestet – und wir können das Resultat mit unserem Testprogramm verifizieren:
Beispiel:
void calcPalindrom(const Number& start, size_t count)
{
std::tuple<std::optional<Number>, Number, size_t> result{
PalindromCalculator::calcPalindrom(start, count)
};
std::cout
<< "Searching palindrom beginning at " << std::get<1>(result)
<< " [" << std::get<2>(result) << " steps]:" << std::endl;
if (std::get<0>(result).has_value()) {
std::cout << "Found palindrom: " << std::get<0>(result).value() << std::endl;
}
else {
std::cout << "No palindrom found!" << std::endl;
}
}
void Test_Palindrom()
{
Number start{ "1.186.060.307.891.929.990" };
size_t count{ 270 };
calcPalindrom(start, count);
}
Ausgabe:
Searching palindrom beginning at 1.186.060.307.891.929.990 [261 steps]:
Found palindrom:
44.562.665.878.976.437.622.437.848.976.653.870.388.884.783.662.
598.425.855.963.436.955.852.489.526.638.748.888.307.835.667.
984.873.422.673.467.987.856.626.544
Auch findet man unter What is a Palindrome? „Weltrekorde” dokumentiert vor:
THE NEW WORLD RECORD (Jan 4, 2021)
Anton Stefanov has discovered the new World Record!
The 23 digit number 13968441660506503386020 solves after 289 iterations to form a 142 digit palindrome!
Das wollen wir doch glattweg überprüfen und schmeißen unsere Realisierung mit dem Startwert 13.968.441.660.506.503.386.020 an:
void Test_Palindrom()
{
Number start{ "13.968.441.660.506.503.386.020" };
size_t count{ 300 };
calcPalindrom(start, count);
}
Ausgabe:
Searching palindrom beginning at 13.968.441.660.506.503.386.020 [289 steps]:
Found palindrom:
6.634.343.445.544.188.178.365.154.497.662.249.922.269.477.578.
658.488.045.222.897.505.659.677.887.769.565.057.982.225.408.
848.568.757.749.622.299.422.667.944.515.638.718.814.455.443.
434.366
Vielleicht finden Sie mit Hilfe dieses Lösungsvorschlags neue Weltrekorde :)