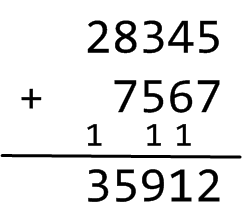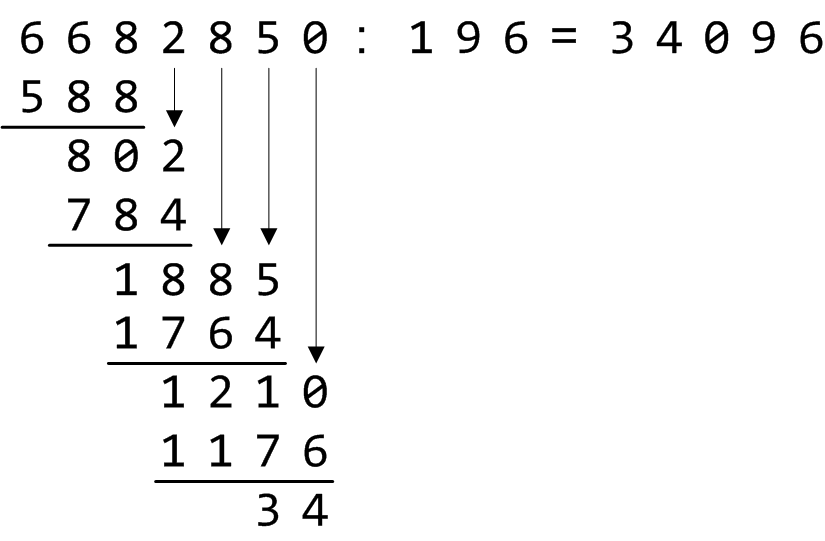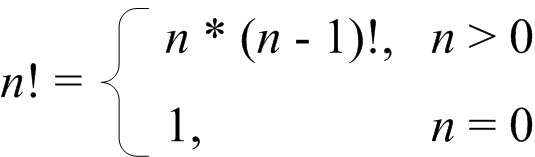Die ganzzahligen Standarddatentypen in C++ wie short, int usw. besitzen allesamt die Eigenschaft, dass ihr Wertebereich limitiert ist. Für viele Anwendungen ist dies nicht nachteilig, da sich speziell mit den Datentypen int und long oder auch size_t ziemlich große Zahlen darstellen lassen. Für manche Anwendungen ist die Verarbeitung von ganzen Zahlen beliebiger Größe jedoch unabdingbar. Wir stellen im Folgenden eine Klasse BigInteger vor, die eine exakte Arithmetik vorzeichenbehafteter ganzer Zahlen beliebiger Größe zur Verfügung stellt.

Lernziele

Funktor einer Klasse
Container std::vector<T>
Klasse string_view
Benutzerdefiniertes Literal (hier: _big)
Lambda-Funktionen (mit mutable)
Datentyp uint8_t
Verschiebesemantik mit std::move
Einsatz von std::reverse_iterator
Werfen von Ausnahmen mit throw und std::invalid_argument
STL-Algorithmen bzw. -Funktionen std::for_each, std::find_if, std::begin, std::end, std::rbegin, std::rend, std::isdigit und std::remove

Grundgerüst der Klasse `BigInteger`

Um potentiell beliebig viele Ziffern einer sehr großen Zahl in einem BigInteger-Objekt abzulegen, gibt es mehrere Möglichkeiten wie etwa die Verwendung (generischer) Standardcontainer aus der STL (C++ Standard Template Library) oder auch einfach nur die Ablage der Ziffern in einer Zeichenkette. In der vorgestellten Lösung legen wir auf ein std::vector<T>-Objekt zugrunde.

Unsere Kenntnisse aus der Schulmathematik zur schriftlichen Addition, Multiplikation usw. stellen die Grundlage für die Implementierung der arithmetischen Operatoren in der BigInteger-Klasse dar. Vermutlich sind Ihre Erinnerungen hierzu, wie meine auch, zwischenzeitlich recht verschwommen. In den nachfolgenden Hinweisen finden Sie einen kurzen Auffrischungskurs dieser schulmathematischen Grundlagen vor.

Um etwaige Missverständnisse rechtzeitig auszuräumen: In der Implementierung Ihrer Klasse BigInteger dürfen Sie zum Rechnen mit einzelnen Ziffern – aus denen die „sehr großen Zahlen” gebildet werden – selbstverständlich die Standardoperatoren von C++ wie + oder * verwenden. Ziel dieser Fallstudie ist es, einen Klassentyp zu entwickeln, der die Wertebereichslimitierungen dieser elementaren ganzzahligen Datentypen überwindet.

Erste Hinweise zur BigInteger-Klasse finden Sie in Tabelle 1 vor:

Element	Beschreibung
Konstruktor	`BigInteger();` Erzeugt ein `BigInteger`-Objekt zur Zahl 0.
Benutzerdefinierter Konstruktor	`explicit BigInteger(std::string_view);` Erzeugt ein `BigInteger`-Objekt mit Hilfe der Beschreibung einer Zahl in Form einer Zeichenkette.
Konvertierungs-Konstruktor	`explicit BigInteger(int);` Erzeugt ein `BigInteger`-Objekt anhand eines `int`-Werts.
Konvertierungs-Konstruktor	`explicit BigInteger(long);` Erzeugt ein `BigInteger`-Objekt anhand eines `long`-Werts.
Konvertierungs-Konstruktor	`explicit BigInteger(long long);` Erzeugt ein `BigInteger`-Objekt anhand eines `long long`-Werts.

Tabelle 1: Konstruktoren der Klasse BigInteger.

Eine Zeichenkette zur Beschreibung eines BigInteger-Objekts darf optional mit einem Plus- oder Minuszeichen beginnen, um das Vorzeichen der Zahl festzulegen. Danach folgen beliebig viele dezimale Ziffern:

BigInteger a { "+11111111111111111111111111111111111111" };

Mit Ausnahme von Punkten dürfen in der Zeichenkette keine anderen Zeichen enthalten sein. Punkte sind der besseren Lesbarkeit halber in der Zeichenkette zulässig, wie etwa "123.456.789".

Eine zweite Möglichkeit zum Benutzen von BigInteger-Objekten sind ab C++ 11 die so genannten „benutzerdefinierte Literale”. Diese gestatten es, einen konstanten Wert der jeweiligen Klasse, also BigInteger in unserem Fall, mit einem Suffix in das Lexikon von C++ aufzunehmen. Wenn wir uns auf das Suffix _big festlegen, dann sind die folgenden Anweisungen gültiges C++:

BigInteger n{};
n = 1_big;
n = 1234567890_big;
n = -1234567890_big;
n = 111111111111111111111111111111111111111111111111111111_big;
n = 111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111_big;

In der letzten Wertzuweisung erkennen wir eine weitere Neuerung von C++: In konstanten ganzzahligen Werten – und damit auch in benutzerdefinierten Literalen – können Einzelhochkommata zur besseren Lesbarkeit eingefügt werden. Damit kein Missverständnis entsteht:

Im Konstruktor der Klasse BigInteger mit einem std::string_view-Objekt als Parameter haben wir uns auf den Punkt . als zulässiges Trennzeichen festgelegt. Theoretisch hätten wir uns auch für ein anderes Trennzeichen entscheiden können. Es bleibt der Realisierung des Konstruktors überlassen, diese Trennzeichen herauszufiltern und zu ignorieren.
Benutzerdefinierte Literale der Klasse BigInteger werden vom C++-Scanner analysiert, hier ist der Punkt deshalb unzulässig, dafür aber das Hochkomma. Allerdings werden die Hochkommata an die Realisierung des korrespondierenden C++-Operators durchgereicht, also ist auch in diesem Fall eine Sonderbehandlung notwendig.

Damit stellt sich die Frage nach der Realisierung eines derartigen Suffixes für literale BigInteger-Objekte: Es ist der sogenannte Literaloperator operator"" mit folgender Schnittstelle zu implementieren:

BigInteger operator"" _big(const char* literal);

Bei einem Literal 1234567890_big wird der Literaloperator mit dem Parameter "1234567890" aufgerufen.

Anmerkung: Es ist eine Restriktion des Microsoft Visual C++ Compilers, dass benutzerdefinierte Literale mit einem Unterstrich '_' anfangen müssen.

Damit sind wir bei den getter-Methoden der Klasse BigInteger angekommen, sie sind in Tabelle 2 beschrieben:

Element	Beschreibung
getter `size()`	`size_t size() const;` Liefert die Anzahl der Ziffern der Zahl, auch Stelligkeit der ganzen Zahl genannt, zurück.
getter `zero()`	`bool zero() const;` Liefert den Wert `true` zurück, wenn die Zahl 0 ist, andernfalls `false`.
getter `sign()`	`bool sign() const;` Liefert das Vorzeichen der Zahl zurück, `true` entspricht einer positiven Zahl, `false` einer negativen.

Tabelle 2: getter-Methoden der Klasse BigInteger.

Ausgabe

Zur Ausgabe eines BigInteger-Objekts auf der Konsole mit dem Standardobjekt std::cout ist der <<-Operator geeignet zu überladen. Um die Lesbarkeit der Zeichenfolge zu steigern, ist nach jeder dritten Stelle ein Punkt einzufügen, also zum Beispiel "99.999".

Arithmetische Operatoren der Klasse `BigInteger`

Wir geben nun einige Hinweise zu den Grundrechenarten, wie sie in der Schulmathematik gelehrt werden. Bei der so genannten schriftlichen Addition werden die zu addierenden Zahlen rechtsbündig so angeordnet, dass jeweils gleichwertige Ziffern untereinander stehen (Einer unter Einer, Zehner unter Zehner usw.). Man addiert dann die jeweils untereinander stehenden Ziffern, beginnend mit den Einern. Ergeben die addierten Ziffern eine Zahl größer oder gleich 10, berücksichtigt man den Übertrag bei der Addition der nächsten zwei Ziffern, siehe Abbildung 1:

/img/biginteger/Schulmathematik_Addition_01.png

Abbildung 1: Schriftliche Addition der Schulmathematik.

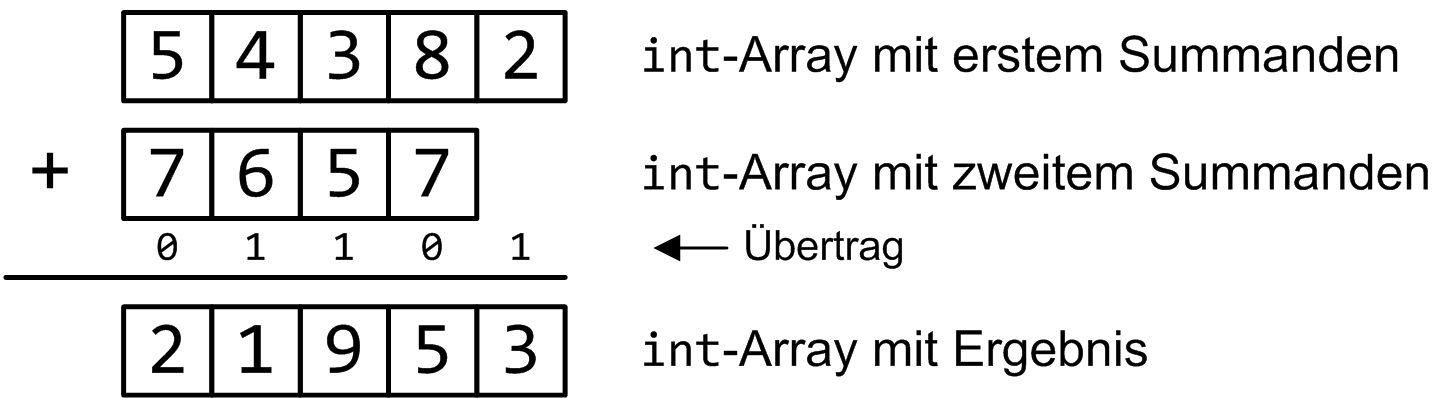
Bei der Umsetzung der schriftlichen Addition in einem C++-Programm stellt sich die Frage, in welcher Reihenfolge die einzelnen Ziffern im korrespondierenden std::vector<T>-Objekt abgelegt werden. Da die einzelnen Ziffern stellenweise, beginnend mit der niedrigstwertigen Stelle, zu addieren sind, bietet es sich an, die einzelnen Ziffern in umgekehrter Reihenfolge im Container abzuspeichern. Wenn wir das Beispiel aus Abbildung 1 noch einmal betrachten, so würde die Ablage und Verarbeitung der beiden Zahlen 28345 und 7567 in einem BigInteger-Objekt wie in Abbildung 2 gezeigt aussehen:

/img/biginteger/Schulmathematik_Addition_02.png

Abbildung 2: Ablage der Ziffern in umgekehrter Reihenfolge.

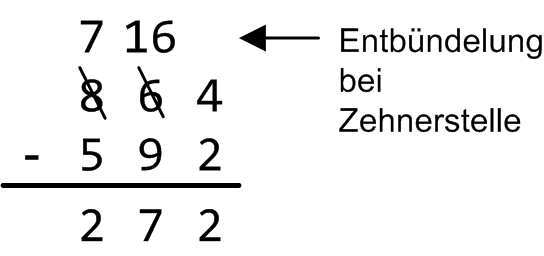
Die schriftliche Subtraktion funktioniert prinzipiell zunächst einmal so wie die schriftliche Addition. Beginnend mit der niedrigstwertigen Stelle wird Stelle für Stelle die Ziffer des Subtrahenden (untere Ziffer) von der Ziffer des Minuenden (obere Ziffer) abgezogen. Ein Problem entsteht, wenn die obere Ziffer kleiner ist als die dazugehörige untere des Subtrahenden, so dass die Subtraktion der zwei Ziffern nicht durchgeführt werden kann. Hier gibt es mehrere Verfahren zur Lösung des Problems. Wir skizzieren im Folgenden das so genannte Entbündelungsverfahren. Subtrahieren mit Entbündeln bedeutet, dass der zu kleine Minuend bei seinem linken Nachbarn eine „Anleihe” macht. Durch Borgen von der nächsthöheren Stelle wird die Ziffer des Minuenden um 10 erhöht, und zum Zwecke des Ausgleichs die nächsthöherwertige Ziffer des Minuenden um 1 erniedrigt. Auf diese Weise kann man stets erreichen, dass die untenliegende Ziffer von der obenliegenden abgezogen werden kann, wie wir im Beispiel aus Abbildung 3 vorführen:

/img/biginteger/Schulmathematik_Subtraktion_01.png

Abbildung 3: Entbündelungsverfahren für Subtraktion.

Die Subtraktion der Einerstelle in Abbildung 3 bereitet keine Probleme, 4 minus 2 ist gleich 2. Die Zehnerstellen lassen sich zunächst nicht abziehen, der Minuend 6 ist zu klein. Er wird darum um 10 erhöht, also gleich 16 gesetzt. Diese 10 wird von der links daneben stehenden Ziffer 8 geliehen und deshalb wird diese um 1 erniedrigt (neuer Wert 7). Nun können die nächsten zwei Subtraktionen (16 minus 9 und 7 minus 5) problemlos durchgeführt werden und man erhält 272 als korrektes Gesamtergebnis der Subtraktion.

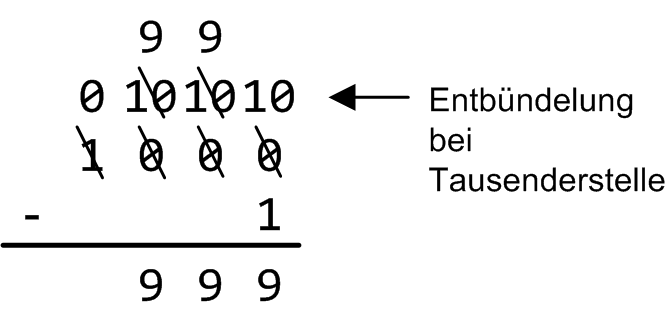
Hinweis: Einen Sonderfall müssen Sie in Ihrer Implementierung noch beachten, nämlich wenn beim Leihen die korrespondierende Ziffer des Minuenden gleich 0 ist. Von 0 lässt sich bekanntermaßen nichts borgen (ein Wert -1 stellt hier keine Lösung des Problems dar), es muss folglich Stelle für Stelle in Richtung der höherwertigen Stellen solange weitergesucht werden, bis eine erste Ziffer ungleich 0 vorliegt. Nun kann hier der Leihvorgang stattfinden und der geliehene Wert über alle Zwischenstellen nach unten durchgereicht werden. In Abbildung 4 finden Sie ein Beispiel für diese Situation vor. Um 1 von 1000 abziehen zu können, muss zum Leihen drei Stellen nach links gegangen werden:

/img/biginteger/Schulmathematik_Subtraktion_02.png

Abbildung 4: Entbündelungsverfahren mit Null als linkem Nachbarn.

Damit sind wir bei der Multiplikation angekommen. Das Standardverfahren beruht darin, die erste Zahl mit den einzelnen Ziffern der zweiten Zahl nacheinander, beginnend bei der letzten Stelle, zu multiplizieren. Für jede neue Ziffer wird eine neue Zeile benötigt. Man schreibt jede Multiplikation untereinander und addiert die einzelnen Werte. Wie bei der Addition ist auch bei der Multiplikation ein Überlauf auf die jeweils nächsthöhere Stelle zu übertragen.

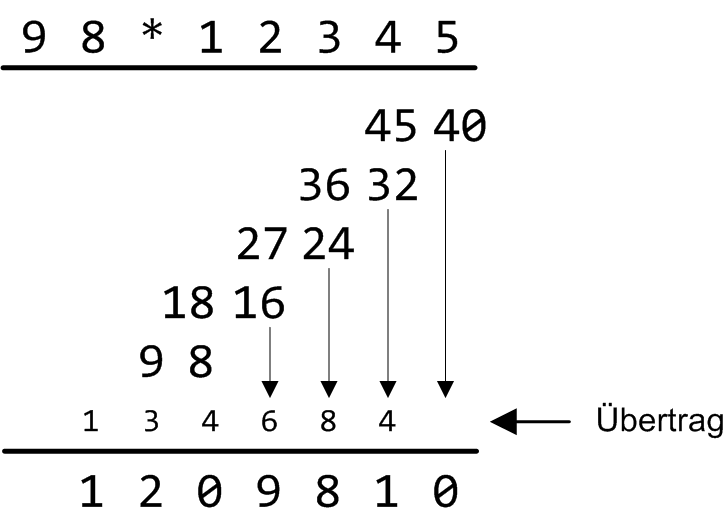
Im Gegensatz zum Standardverfahren der Schulmathematik vereinfachen wir das Verfahren dahingehend, dass wir in den einzelnen Zeilen keinen Überlauf berücksichtigen. Dies tun wir erst, wenn wir die Zwischenresultate der einzelnen Zeilen Spalte für Spalte, von rechts beginnend, zusammenzählen. Am Beispiel von 98 * 12345 können Sie den Algorithmus in Abbildung 5 nachverfolgen:

/img/biginteger/Schulmathematik_Multiplikation.png

Abbildung 5: Standardverfahren für schriftliche Multiplikation.

Wir schließen diese Betrachtungen mit der schriftlichen Division ab. Bezüglich der Namensgebung rekapitulieren wir zunächst einmal, dass ein Dividend durch einen Divisor geteilt wird, das Ergebnis heißt Quotient, der in unserem Fall stets ganzzahlig ist und aus diesem Grund in den meisten Fällen noch um einen Rest zu ergänzen ist. Wir beginnen mit der ersten (führenden) Zahl des Dividenden. Ist diese Zahl nicht größer als der Divisor, nehmen wir die nächste Zahl des Dividenden mit hinzu und wiederholen diesen Vorgang solange, bis die auf diese Weise gebildete Zahl größer ist als der Dividend. Nun teilen wir diese Zahl durch den Divisor, das Ergebnis bildet die erste Ziffer des gesuchten Quotienten. Um die Division fortsetzen zu können, multiplizieren wir das Ergebnis mit dem Divisor, und subtrahieren das Produkt von der alten Zahl. Das so erhaltene Ergebnis wird durch „Herunterziehen” der nächsten Ziffer von oben ergänzt. Dieses Procedere beginnen wir nun wieder von vorne. Der neue Dividend ist das Ergebnis der letzten Subtraktion, ergänzt um die heruntergezogene Ziffer usw.

Das ganze Verfahren wird solange wiederholt, bis alle Stellen des Dividenden nach unten gezogen wurden. Die unterste Zahl stellt den Rest der Division dar, der gesuchte Quotient wurde Ziffer für Ziffer zusammengesetzt. Möglicherweise ist diese textuelle Beschreibung des Divisionsalgorithmus etwas schwer verdaulich, zur Illustration betrachten wir in Abbildung 6 das folgende Beispiel:

/img/biginteger/Schulmathematik_Division.png

Abbildung 5: Standardverfahren der schriftlichen Division.

Nach diesen Hilfestellungen fassen wir die soeben besprochenen arithmetischen Operatoren für eine Ergänzung der BigInteger-Klasse in Tabelle 3 zusammen:

Operator	Beschreibung
Operator `+`	`friend BigInteger operator+ (const BigInteger& a, const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert sich aus der Addition von `a` und `b` ergibt.
Operator `-`	`friend BigInteger operator- (const BigInteger& a, const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert sich aus der Subtraktion von `a` und `b` ergibt.
Operator `*`	`friend BigInteger operator* (const BigInteger& a, const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert sich aus der Multiplikation von `a` und `b` ergibt.
Operator `/`	`friend BigInteger operator/ (const BigInteger& a, const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert sich aus der Division von `a` und `b` ergibt.
Operator `%`	`friend BigInteger operator% (const BigInteger& a, const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert sich aus dem Rest bei Division von `a` und `b` ergibt.

Tabelle 3: Arithmetische Operatoren der Klasse BigInteger.

Neben den arithmetischen Operatoren der Klasse BigInteger gibt es natürlich auch noch die entsprechenden arithmetischen Wertzuweisungsoperatoren wie zum Beispiel +=, siehe hierzu Tabelle 4:

Operator	Beschreibung
Operator `+`	`friend BigInteger& operator+= (BigInteger& a, const BigInteger& b);` Addition von `a` und `b` mit Zuweisung an `a`.
Operator `-`	`friend BigInteger& operator-= (BigInteger& a, const BigInteger& b);` Subtraktion von `a` und `b` mit Zuweisung an `a`.
Operator `*`	`friend BigInteger& operator*= (BigInteger& a, const BigInteger& b);` Multiplikation von `a` und `b` mit Zuweisung an `a`.
Operator `/`	`friend BigInteger& operator/= (BigInteger& a, const BigInteger& b);` Division von `a` und `b` mit Zuweisung an `a`.
Operator `%`	`friend BigInteger& operator%= (BigInteger& a, const BigInteger& b);` Rest bei Division von `a` und `b` mit Zuweisung an `a`.

Tabelle 4: Arithmetische Wertzuweisungsoperatoren der Klasse BigInteger.

In den meisten Situationen denken wir bei arithmetischen Operatoren an ihre binäre Variante. Ganze – und damit auch sehr große ganze – Zahlen können auch ein Vorzeichen haben: + oder -. Für diese beiden Fälle benötigen wir jeweils den +– oder -–Operator in seiner unären Ausprägung (Tabelle 5):

Operator	Beschreibung
Operator `+`	`friend BigInteger operator+ (const BigInteger& a);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert eine Kopie von `a` ist.
Operator `-`	`friend BigInteger operator- (const BigInteger& b);` Liefert ein neues `BigInteger`-Objekt zurück, dessen Wert eine negative Kopie von `a` ist.

Tabelle 5: Unäre arithmetische Operatoren der Klasse BigInteger.

Bemerkung: Der unäre +-Operator ist eigentlich unnötig; ich habe ihn jedoch aus Symmetriegründen in der Klasse BigInteger mit eingeführt. Auch ließe sich darüber diskutieren, ob das unäre Plus eine Referenz des aktuellen Objekts oder eine Kopie dessen zurückliefert. Wiederum aus Symmetriegründen zum --Operator wollte ich beide Realisierungen identisch halten.

Vergleichsoperatoren der Klasse `BigInteger`

Große Zahlen kann man vergleichen, etwa auf Gleichheit oder auf kleiner(-gleich) und größer(-gleich). Entsprechende Operatoren hierzu sind in Tabelle 6 festgelegt:

Operator	Beschreibung
Operator `==`	`friend bool operator== (const BigInteger& a, const BigInteger& b);` Vergleicht den Wert zweier `BigInteger`-Objekte `a` und `b` auf Gleichheit.
Operator `!=`	`friend bool operator!= (const BigInteger& a, const BigInteger& b);` Vergleicht den Wert zweier `BigInteger`-Objekte `a` und `b` auf Ungleichheit.
Operator `<`	`friend bool operator< (const BigInteger& a, const BigInteger& b);` Umsetzung der mathematischen Relation kleiner.
Operator `<=`	`friend bool operator<= (const BigInteger& a, const BigInteger& b);` Umsetzung der mathematischen Relation kleiner-gleich.
Operator `>`	`friend bool operator> (const BigInteger& a, const BigInteger& b);` Umsetzung der mathematischen Relation größer.
Operator `>=`	`friend bool operator>= (const BigInteger& a, const BigInteger& b);` Umsetzung der mathematischen Relation größer-gleich.

Tabelle 6: Vergleichsoperatoren der Klasse BigInteger.

Hilfsmethoden der Klasse `BigInteger`

Möglicherweise benötigen Sie zur Implementierung der vorangestellten Abschnitte noch die eine oder andere Hilfsmethode. Bei den arithmetischen Operationen können beispielsweise in manchen Situationen im internen std::vector<T>-Objekt führende Nullen entstehen. Im Extremfall kann man dies bei der Subtraktion einer Zahl mit sich selbst beobachten, also etwa 100 - 100. Das Ergebnis sollte dann nicht 000, sondern eben 0 lauten. Zur Behebung dieser Unschönheit finden Sie in Tabelle 7 die Methode removeLeadingZeros nebst einigen weiteren Methoden vor:

Methode	Beschreibung
Methode `removeLeadingZeros`	`void removeLeadingZeros();` Entfernt führende Nullen im internen `std::vector<T>`-Objekt eines `BigInteger`-Objekts.
Methode `abs`	`BigInteger abs() const;` Liefert ein `BigInteger`-Objekt mit dem Absolutbetrag des aktuellen Objekts zurück.
Methode `pow`	`BigInteger pow(int n);` Liefert ein `BigInteger`-Objekt zurück, das die Basis (`this`) potenziert mit dem Exponenten `n` repräsentiert – also `this`ⁿ.

Tabelle 7: Hilfsmethoden der Klasse BigInteger.

Einige Beispiele

Beispiel:

// testing c'tors
BigInteger n1{ "1234567" };
std::cout << n1 << std::endl;

BigInteger n2{ "-1234567" };
std::cout << n2 << std::endl;

BigInteger n3{ "123.456.789.012.345.678" };
std::cout << n3 << std::endl;

Ausgabe:

1.234.567
-1.234.567
123.456.789.012.345.678

Beispiel:

// testing literals
BigInteger n{};

n = 1_big;
std::cout << n << std::endl;

n = 1234567890_big;
std::cout << n << std::endl;

n = -1234567890_big;
std::cout << n << std::endl;

n = 111111111111111111111111111111111111111111111111111111_big;
std::cout << n << std::endl;

n = 111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111'111_big;
std::cout << n << std::endl;

Ausgabe:

1
1.234.567.890
-1.234.567.890
111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111
111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111.111

Beispiel:

// testing addition
BigInteger n1{ "11111111" };
BigInteger n2{ "22222222" };
std::cout << n1 << " + " << n2 << " = " << n1 + n2 << std::endl;

n1 = BigInteger{ "99999999999999" };
n2 = BigInteger{ "1" };
std::cout << n1 << " + " << n2 << " = " << n1 + n2 << std::endl;

Ausgabe:

11.111.111 + 22.222.222 = 33.333.333
99.999.999.999.999 + 1 = 100.000.000.000.000

Beispiel:

// testing subtraction
BigInteger n1{ "999" };
BigInteger n2{ "900" };
std::cout << n1 << " - " << n2 << " = " << n1 - n2 << std::endl;

n1 = BigInteger{ "999" };
n2 = BigInteger{ "998" };
std::cout << n1 << " - " << n2 << " = " << n1 - n2 << std::endl;

n1 = BigInteger{ "999" };
n2 = BigInteger{ "999" };
std::cout << n1 << " - " << n2 << " = " << n1 - n2 << std::endl;

n1 = BigInteger{ "11111" };
n2 = BigInteger{ "222" };
std::cout << n1 << " - " << n2 << " = " << n1 - n2 << std::endl;

n1 = BigInteger{ "1000000" };
n2 = BigInteger{ "1" };
std::cout << n1 << " - " << n2 << " = " << n1 - n2 << std::endl;

Ausgabe:

999 - 900 = 99
999 - 998 = 1
999 - 999 = 0
11.111 - 222 = 10.889
1.000.000 - 1 = 999.999

Lösung

Quellcode: Siehe auch Github.

Die Realisierung der Klasse BigInteger ist nicht in allen Teilen trivial. Wir gehen die einzelnen Abschnitte detailliert durch. Die notwendigen Instanzvariablen der Klasse BigInteger wurden durch die Aufgabenstellung mehr oder minder nahe gelegt:

std::vector<DigitType> m_digits;
bool m_sign;

Die einzelnen Ziffern der großen Zahl werden in einem Array des Typs std::vector<DigitType> abgelegt. Hier hätte man vielleicht der Einfachheit halber einen Typ std::vector<int> erwartet. Da wir es möglicherweise mit sehr vielen Ziffern zu tun haben, die im Speicher dicht gepackt und konsekutiv abgelegt werden sollten, wollen wir hier platzsparend vorgehen. Mit einer Typdefinition

using digit_t = uint8_t;

können wir diese Anforderung erzielen und die Festlegung auch variabel (bzgl. der Übersetzungszeit) gestalten. Für das Vorzeichen der Zahl benötigen wir eine zusätzliche Instanzvariable m_sign, der Datentyp bool gestattet es, positive Zahlen mit dem Wert true und negative Zahlen mit false zu assoziieren.

In Listing 1 beginnen wir unseren Parcours durch den Lösungsteil mit der Schnittstelle der Klasse BigInteger:

01: using digit_t = uint8_t;
02: 
03: class BigInteger
04: {
05: private:
06:     std::vector<digit_t> m_digits;
07:     bool m_sign;
08: 
09: public:
10:     // c'tors / d'tor
11:     BigInteger();
12:     explicit BigInteger(std::string_view);
13: 
14:     // type conversion c'tors
15:     explicit BigInteger(int);
16:     explicit BigInteger(long);
17:     explicit BigInteger(long long);
18: 
19: public:
20:     // getter
21:     size_t size() const;
22:     bool zero() const;
23:     bool sign() const;
24: 
25:     // comparison operators
26:     friend bool operator== (const BigInteger&, const BigInteger&);
27:     friend bool operator!= (const BigInteger&, const BigInteger&);
28:     friend bool operator<  (const BigInteger&, const BigInteger&);
29:     friend bool operator<= (const BigInteger&, const BigInteger&);
30:     friend bool operator>  (const BigInteger&, const BigInteger&);
31:     friend bool operator>= (const BigInteger&, const BigInteger&);
32: 
33:     // unary arithmetic operators
34:     friend BigInteger operator+ (const BigInteger&);
35:     friend BigInteger operator- (const BigInteger&);
36: 
37:     // binary arithmetic operators
38:     friend BigInteger operator+ (const BigInteger&, const BigInteger&);
39:     friend BigInteger operator- (const BigInteger&, const BigInteger&);
40:     friend BigInteger operator* (const BigInteger&, const BigInteger&);
41:     friend BigInteger operator/ (const BigInteger&, const BigInteger&);
42:     friend BigInteger operator% (const BigInteger&, const BigInteger&);
43: 
44:     // arithmetic-assignment operators
45:     friend BigInteger& operator+= (BigInteger&, const BigInteger&);
46:     friend BigInteger& operator-= (BigInteger&, const BigInteger&);
47:     friend BigInteger& operator*= (BigInteger&, const BigInteger&);
48:     friend BigInteger& operator/= (BigInteger&, const BigInteger&);
49:     friend BigInteger& operator%= (BigInteger&, const BigInteger&);
50: 
51:     // increment/decrement operators (prefix/postfix version)
52:     friend BigInteger& operator++ (BigInteger&);       // prefix increment
53:     friend BigInteger  operator++ (BigInteger&, int);  // postfix increment
54:     friend BigInteger& operator-- (BigInteger&);       // prefix decrement
55:     friend BigInteger  operator-- (BigInteger&, int);  // postfix decrement
56: 
57:     // type conversion operators
58:     operator int() const;
59:     operator long() const;
60:     operator long long() const;
61: 
62:     // functor (supporting formatted output)
63:     std::string operator()(int);
64: 
65:     // public helper methods
66:     BigInteger abs() const;
67:     BigInteger pow(int);
68: 
69: private:
70:     // private helper operator
71:     digit_t& operator[] (size_t);  // subscript operator
72:     const digit_t& operator[] (size_t) const; // const subscript operator
73: 
74:     // private helper methods
75:     void removeLeadingZeros();
76:     int compareTo(const BigInteger&) const;
77:     void toBigInteger(long long);
78:     long long toLongLong() const;
79: 
80:     // output
81:     friend std::ostream& operator<< (std::ostream&, const BigInteger&);
82: };
83: 
84: BigInteger operator"" _big(const char*);

Listing 1: Schnittstelle der Klasse BigInteger.

Der Standardkonstruktor soll die Zahl 0 repräsentieren, dazu benötigen wir immerhin ein Ziffernfeld der Länge 1:

// default c'tor
BigInteger::BigInteger() : m_digits{ 1 }, m_sign{ true } {
    m_digits[0] = 0; 
}

Der wichtigste Konstruktor der BigInteger-Klasse erwartet eine (beliebig lange) Zeichenkette und kopiert ihren Inhalt, abgesehen von den Punkten '.' für die verbesserte Lesbarkeit der Eingabe, in das m_digits-Vektorobjekt um. Da wir im Prinzip nur konstante Zeichenketten erwarten (oder unterstützen), ist der Parameter vom Typ std::string_view. std::string_view-Objekte sind eine optimierte Version der Klasse std::string, sie bestehen ausschließlich aus einem raw-Zeiger einer konstanten Zeichenkette und einer Längenangabe. Prinzipiell wird von der Zeichenkette erwartet, dass diese korrekt aufgebaut ist. Im Fehlerfall wird eine Ausnahme des Typs std::invalid_argument geworfen (siehe die Zeilen 10 und 23 von Listing 2):

01: BigInteger::BigInteger(std::string_view sv) : m_sign{ true }
02: {
03:     std::reverse_iterator<std::string_view::iterator> r = sv.rbegin();
04: 
05:     std::for_each(std::rbegin(sv), std::prev(std::rend(sv)), [this](char ch) {
06:         if (ch == '.') {
07:             return;
08:         }
09:         else if (! std::isdigit(ch)) {
10:             throw std::invalid_argument("illegal digit in big number");
11:         }
12:         else {
13:             m_digits.push_back(ch - '0');
14:         }
15:     });
16: 
17:     char ch = *std::prev(std::rend(sv));
18:     if (ch == '+' or ch == '-') {
19:         m_sign = (ch == '-') ? false : true;
20:     }
21:     else {
22:         if (!std::isdigit(ch)) {
23:             throw std::invalid_argument("illegal digit in big number");
24:         }
25:         m_digits.push_back(ch - '0');
26:     }
27: 
28:     removeLeadingZeros();
29: }

Listing 2: Benutzerdefinierter Konstruktor der Klasse BigInteger.

Da wir die Ziffern eines BigInteger-Objekts intern in der umgekehrten Reihenfolge ablegen, kommt ein std::reverse_iterator zum Einsatz.

Nach der Erzeugung eines BigInteger-Objekts an Hand einer Zeichenkette kommen wir gleich auf die entgegengesetzte Operation zu sprechen: Umwandlung eines BigInteger-Objekts in eine Zeichenkette. Diese Operation haben wir im Funktor der Klasse untergebracht. Dieser ist flexibel in der Aufnahme von Parameterwerten. Wir definieren ihn mit einem Parameter vom Typ int, um die Anzahl der Dreiziffernblöcke pro Zeile festzulegen. Die Zeilen 10 bis 48 (Listing 3) widmen sich dem Umstand, mit wie vielen Leerzeichen der erste Dreiziffernblock aufzufüllen ist, wenn die Anzahl der Ziffern kein Vielfaches von 3 ist. Da auch noch ein mögliches Vorzeichen zu berücksichtigen ist, gewinnt der Sourcecode leider nicht gerade an Übersichtlichkeit.

01: // functor (supporting formatted output)
02: std::string BigInteger::operator()(int n)
03: {
04:     std::string firstSuffix{};
05:     std::string subsequentSuffix{ std::string {" "} };
06: 
07:     std::string result{};
08:     int skippedDigits{};
09: 
10:     if (! m_sign) {
11:         firstSuffix = std::string{ "-" };
12:         subsequentSuffix = std::string{ "  " };
13:     }
14: 
15:     std::reverse_iterator<std::vector<digit_t>::iterator> rev_it = std::rbegin(m_digits);
16: 
17:     // calculate suffix of output
18:     if (size() % 3 == 0) {
19:         char digit1 = m_digits.rbegin()[0] + '0'; // ultimate element
20:         char digit2 = m_digits.rbegin()[1] + '0'; // penultimate element
21:         char digit3 = m_digits.rbegin()[2] + '0'; // pen-penultimate element
22:         firstSuffix.push_back(digit1);
23:         firstSuffix.push_back(digit2);
24:         firstSuffix.push_back(digit3);
25:         subsequentSuffix.append("   ");
26:         rev_it += 3;
27:         skippedDigits = 3;
28:     }
29:     else if (size() % 3 == 1) {
30:         char digit1 = m_digits.rbegin()[0] + '0'; // ultimate element
31: 
32:         firstSuffix.push_back(digit1);
33: 
34:         subsequentSuffix.append(" ");
35:         rev_it += 1;
36:         skippedDigits = 1;
37:     }
38:     else if (size() % 3 == 2) {
39:         char digit1 = m_digits.rbegin()[0] + '0'; // ultimate element
40:         char digit2 = m_digits.rbegin()[1] + '0'; // penultimate element
41: 
42:         firstSuffix.push_back(digit1);
43:         firstSuffix.push_back(digit2);
44: 
45:         subsequentSuffix.append("  ");
46:         rev_it += 2;
47:         skippedDigits = 2;
48:     }
49: 
50:     result = firstSuffix;
51:     result.push_back('.');
52: 
53:     int blocks{ 0 };
54: 
55:     std::for_each(
56:         rev_it,
57:         std::rend(m_digits),
58:         [&, i = m_digits.size() - skippedDigits - 1](int digit) mutable {
59:         result.push_back ((char)(digit + '0'));
60:         if (i > 0 && i % 3 == 0) {
61:             result.push_back('.');
62:             ++blocks;
63:         }
64:         --i;
65: 
66:         if (blocks == n) {
67:             result.push_back('\n');
68:             blocks = 0;
69:             result.append(subsequentSuffix);
70:         }
71:     });
72: 
73:     return result;
74: }

Listing 3: Wandlung Klasse BigInteger nach std::string.

Laut Spezifikation besitzt die BigInteger-Klasse drei getter-Methoden size, zero und sign, mehr hierzu in Listing 4:

01: bool BigInteger::sign() const { return m_sign; }
02: size_t BigInteger::size() const { return m_digits.size(); }
03: bool BigInteger::zero() const { return m_digits.size() == 1 and m_digits[0] == 0; }

Listing 4: getter-Methoden size, zero und sign der Klasse BigInteger.

Die unären Operatoren + und -, also positives oder negatives Vorzeichen eines BigInteger-Objekts, dürfen in einer korrekten Implementierung nicht fehlen (Listing 5):

01: BigInteger operator+ (const BigInteger& a)
02: {
03:     return { a };
04: }
05: 
06: BigInteger operator- (const BigInteger& a)
07: {
08:     BigInteger tmp{ a };
09: 
10:     if (! a.zero()) {
11:         tmp.m_sign = !tmp.m_sign;
12:     }
13: 
14:     return tmp;
15: }

Listing 5: Unäre Operatoren + und - der Klasse BigInteger.

Beide Operatoren + und - delegieren ihre Arbeit im Wesentlichen an den Kopier-Konstruktor der BigInteger-Klasse. Dieser ist nicht explizit implementiert, da die BigInteger-Klasse entweder aus elementaren Instanzvariablen (hier genügt eine flache Kopie) oder einem std::vector<>-Objekt besteht. Letzteres besitzt seinen eigenen Kopier-Konstruktor, dieser wird beim Kopieren eines BigInteger-Objekts in Anspruch genommen.

Damit sind wir beim Kernstück der BigInteger-Klasse angekommen, ihren arithmetischen Operatoren. Die Addition großer Zahlen entnehmen Sie bitte Listing 6:

01: BigInteger operator+ (const BigInteger& a, const BigInteger& b)
02: {
03:     // handle sign and change operation
04:     if (a.sign() != b.sign())
05:         return (a.sign()) ? a - b.abs() : b - a.abs();
06: 
07:     // need vector
08:     size_t size{ (a.size() >= b.size()) ?
09:         a.size() + 1 :
10:         b.size() + 1 };
11: 
12:     std::vector<digit_t> digits(size);
13: 
14:     // add numbers digit per digit
15:     int carry {};
16:     for (size_t i{}; i != size; i++)
17:     {
18:         if (i < a.size())
19:             carry += a[i];
20:         if (i < b.size())
21:             carry += b[i];
22: 
23:         digits[i] = carry % 10;
24:         carry /= 10;
25:     }
26: 
27:     // move result vector into a BigInteger object
28:     BigInteger tmp{};
29:     tmp.m_digits = std::move(digits);
30:     tmp.m_sign = a.sign();
31:     tmp.removeLeadingZeros();
32:     return tmp;
33: }

Listing 6: Implementierung der Addition großer ganzer Zahlen.

Subtil in Listing 6 sind die zwei Zeilen 4 und 5: Nicht jede Addition zweier ganzer Zahlen ist in Wirklichkeit eine Addition. Je nach Vorhandensein eines negativen Vorzeichens beim ersten oder zweiten Summanden kann auch eine Subtraktion vorliegen. Sollte dies der Fall sein, wird in Zeile 5 an diese weiterverzweigt, die Parameter werden bzgl. ihres Vorzeichens entsprechend angepasst.

Bei der Addition zweier ganzer Zahlen kann man nicht präzise von vorne herein entscheiden, aus wie vielen Ziffern das Resultat besteht. Man kann aber zunächst eine näherungsweise Festlegung treffen, in dem man die Länge des größeren Summanden zu Grunde legt und diese für einen möglichen Überlauf in der letzten Stelle noch um Eins vergrößert, siehe hierzu die Zeilen 8 bis 12. In den Zeilen 15 bis 25 finden Sie die Umsetzung der in Abbildung 1 und Abbildung 2 beschriebenen schulischen Addition vor. Da die Längenabschätzung des Resultat-Vektorobjekts m_digits in den Zeilen 8 bis 12 möglicherweise nicht ganz exakt war, können in dem m_digits-Objekt noch führende Nullen vorhanden sein. Diese werden in Zeile 31 durch einen Aufruf der removeLeadingZeros-Methode entfernt.

Beachten Sie bitte auch Zeile 29: Die Berechnung des Resultats der Addition erfolgte in einem std::vector<> Objekt. Als Rückgabewert der Addition benötigen wir aber ein BigInteger Objekt! In jedem Fall wollen wir vermeiden, dass es bei der Konstruktion dieses Objekts zu einer – unnötigen – Kopie des beteiligten std::vector<>-Objekts kommt. Die Verschiebesemantik ist hierzu angesagt. In Zeile 29 verschieben wir das Resultat-Vektorobjekt mittels des Verschiebewertzuweisungsoperators, der von der Klasse std::vector<> bereitgestellt wird, in das BigInteger-Objekt. Dazu wandeln wir die LValue-Referenz des Arguments digits mit Hilfe von std::move in eine RValue-Referenz um!

Damit sind wir auch schon bei der Subtraktion angekommen, siehe Listing 7:

01: BigInteger operator- (const BigInteger& a, const BigInteger& b)
02: {
03:     // handle sign and change operation
04:     if (a.sign() != b.sign())
05:         return (a.sign()) ? a + b.abs() : -(a.abs() + b);
06: 
07:     if (a.abs() < b.abs())
08:         return (a.sign()) ? -(b - a) : b.abs() - a.abs();
09: 
10:     // create copy of minuend
11:     BigInteger tmp{ a };
12: 
13:     // traverse digits of subtrahend
14:     for (size_t i {}; i != b.size(); ++i)
15:     {
16:         if (tmp[i] < b[i])
17:         {
18:             if (tmp[i + 1] != 0)
19:             {
20:                 tmp[i + 1]--;
21:                 tmp[i] += 10;
22:             }
23:             else
24:             {
25:                 // preceding digit is zero, cannot borrow directly
26:                 size_t pos{ i + 1 };
27:                 while (tmp[pos] == 0)
28:                     pos++;
29: 
30:                 // borrow indirectly
31:                 for (size_t k{ pos }; k >= i + 1; --k)
32:                 {
33:                     tmp[k]--;
34:                     tmp[k - 1] += 10;
35:                 }
36:             }
37:         }
38: 
39:         // subtract current subtrahend digit from minuend digit
40:         tmp[i] -= b[i];
41:     }
42: 
43:     tmp.removeLeadingZeros();
44:     return tmp;
45: }

Listing 7: Implementierung der Subtraktion großer ganzer Zahlen

Die Implementierung der Subtraktion ist im Vergleich zur Addition etwas länger geraten. Die Umsetzung des Entbündelungsverfahrens in den Zeilen 14 bis 22 (Listing 7) ist einfach nachvollziehbar. Kann die Ziffer des Subtrahenden nicht von der korrespondieren Ziffer des Minuenden abgezogen werden, ist etwas mehr Realisierungsaufwand erforderlich, siehe dazu die Zeilen 26 bis 35. Analog zur Addition kann auch bei einer Subtraktion der Fall vorliegen, dass diese in Wirklichkeit einer Addition entspricht. In Zeile 5 erfolgt ein Aufruf der entsprechenden Addition mit bereinigten Vorzeichen. Im anderen Fall lässt die Subtraktion sich auch durchführen, es sind nur Subtrahend und Minuend zu vertauschen und das Vorzeichen des Ergebnisses entsprechend anzupassen. Da das Entbündelungsverfahren nur funktioniert, wenn der Subtrahend kleiner als der Minuend ist, muss auch dieser Fall noch berücksichtigt werden, siehe dazu die Zeilen 7 und 8 von Listing 7.

In Zeile 7 finden wir den <-Operators auf zwei BigInteger-Objekte angewendet vor. Damit sind wir bei den Vergleichsoperatoren angekommen (Listing 8):

bool operator== (const BigInteger& a, const BigInteger& b)
{
    return (a.compareTo(b) == 0) ? true : false;
}

bool operator!= (const BigInteger& a, const BigInteger& b)
{
    return !(a == b);
}

bool operator< (const BigInteger& a, const BigInteger& b)
{
    return (a.compareTo(b) < 0) ? true : false;
}

bool operator<= (const BigInteger& a, const BigInteger& b)
{
    return (a.compareTo(b) <= 0) ? true : false;
}

bool operator> (const BigInteger& a, const BigInteger& b)
{
    return b < a;
}

bool operator>= (const BigInteger& a, const BigInteger& b)
{
    return b <= a;
}

Listing 8: Vergleichsoperatoren der Klasse BigInteger.

Die eigentliche Arbeit, die man zum Vergleichen zweier BigInteger-Objekte anstellen muss, wurde dabei in eine Hilfsmethode compareTo ausgelagert (Listing 9):

01: int BigInteger::compareTo(const BigInteger& a) const 
02: {
03:     if (m_sign && !a.m_sign)
04:         return 1;
05:     if (!m_sign && a.m_sign)
06:         return -1;
07: 
08:     int order = 0;
09:     if (size() < a.size()) {
10:         order = -1;
11:     }
12:     else if (size() > a.size()) {
13:         order = 1;
14:     }
15:     else {
16:         for (size_t i = size() - 1; i != (size_t)-1; --i) {
17:             if (m_digits[i] < a.m_digits[i]) {
18:                 order = -1;
19:                 break;
20:             }
21:             else if (m_digits[i] > a.m_digits[i]) {
22:                 order = 1;
23:                 break;
24:             }
25:         }
26:     }
27: 
28:     return (m_sign) ? order : -order;
29: }

Listing 9: Hilfsmethode compareTo für die Vergleichsoperatoren der Klasse BigInteger.

Da die Ziffern einer großen Zahl intern im BigInteger-Objekt in der umgekehrten Reihenfolge abgelegt werden, ist in der for-Wiederholungsschleife von Listing 9 (Zeile 16) zu beachten, dass die Ziffern von der höchstwertigen bis hin zur niedrigstwertigen Ziffer verglichen werden.

Wir sind etwas vom Thema abgekommen, wir waren bei den arithmetischen Operatoren stehen geblieben und fahren in Listing 10 mit der Multiplikation fort:

01: BigInteger operator* (const BigInteger& a, const BigInteger& b)
02: {
03:     size_t size{ a.size() + b.size() };
04:     std::vector<digit_t> digits(size);
05: 
06:     digit_t carry {};
07:     for (size_t i{}; i != size; ++i) {
08:         digits[i] = carry;
09:         for (size_t j {}; j != b.size(); ++j) {
10:             if (i >= j && i - j < a.size()) {
11:                 digits[i] += a[i - j] * b[j];
12:             }
13:         }
14:         carry = digits[i] / 10;
15:         digits[i] %= 10;
16:     }
17: 
18:     // move result vector into a BigInteger object
19:     BigInteger tmp{};
20:     tmp.m_digits = std::move(digits);
21:     tmp.m_sign = (a.sign() == b.sign()) ? true : false;
22:     tmp.removeLeadingZeros();
23:     return tmp;
24: }

Listing 10: Implementierung der Multiplikation großer ganzer Zahlen.

Wie bei der Addition lässt sich auch bei der Multiplikation die Anzahl der Ziffern des Ergebnisses vor der Rechenoperation nicht ganz exakt bestimmen. Entsprechend legen wir in Zeile 3 ein std::vector<>-Objekt mit der größtmöglichen Länge für die Ziffern an. Einen Strich durch diese Längenberechnung können uns führende Nullen im Ergebnis machen, in Zeile 22 dürfen wir deshalb auf den Aufruf von removeLeadingZeros nicht verzichten.

Der *-Operator ermöglicht eine recht kurze und übersichtliche Realisierung der Methode pow:

01: BigInteger BigInteger::pow(int exponent)
02: {
03:     if (exponent == 0)
04:         return BigInteger{ 1 };
05: 
06:     BigInteger result { *this };
07:     if (exponent == 1)
08:         return result;
09: 
10:     for (int i{ 1 }; i != exponent; i++) {
11:         result = result * *this;
12:     }
13: 
14:     if (!m_sign && exponent % 2 == 1) {
15:         result.m_sign = m_sign;
16:     }
17: 
18:     return result;
19: }

Wir sind fast am Ziel angekommen, es fehlt nur noch die Division (Listing 11):

01: BigInteger operator/ (const BigInteger& a, const BigInteger& b) 
02: {
03:     BigInteger remainder{};
04:     std::vector<digit_t> result;
05: 
06:     // need positive divisor
07:     BigInteger bAbs{ b.abs() };
08: 
09:     size_t pos{ a.size() - 1 };
10: 
11:     while (pos != (size_t)-1) {
12:         // append next digit from dividend to temporary divisor
13:         size_t len{ (remainder.zero()) ? 1 : remainder.size() + 1 };
14:         std::vector<digit_t> digits;
15: 
16:         // copy old digits
17:         for (int k {}; k != len - 1; ++k) {
18:             digits.push_back(remainder[k]);
19:         }
20: 
21:         // fetch digit from dividend
22:         digits.insert(std::begin(digits), a[pos]);
23: 
24:         // move result vector into remainder object
25:         remainder.m_digits = std::move(digits);
26:         remainder.m_sign = true;
27: 
28:         // divide current dividend with divisor
29:         digit_t n {};
30:         while (bAbs <= remainder) {
31:             n++;
32:             remainder -= bAbs;
33:         }
34: 
35:         result.insert(std::begin(result), n);
36: 
37:         --pos; // fetch next digit from divisor
38:     }
39: 
40:     // move result vector into a BigInteger object
41:     BigInteger tmp{};
42:     tmp.m_digits = std::move(result);
43:     tmp.m_sign = (a.sign() == b.sign()) ? true : false;
44:     tmp.removeLeadingZeros();
45:     return tmp;
46: }

Listing 11: Implementierung der Division großer ganzer Zahlen.

Das Ergebnis einer Division wird, wie in Abbildung 6 beschrieben, Ziffer für Ziffer berechnet. Aus diesem Grund bemühen wir in Zeile 35 ein std::vector<>-Objekt, das die einzelnen Ziffern aufnimmt. Ab Zeile 41ff. verschieben wir dieses Objekt in ein BigInteger-Objekt und liefern dieses als Ergebnis der Division zurück. Das Spiegelstück der Division, die Division mit Rest, führt uns zum Modulo-Operator % in Listing 12:

01: BigInteger operator% (const BigInteger& a, const BigInteger& b)
02: {
03:     return a - b * (a / b);
04: }

Listing 12: Implementierung der Division mit Rest (Modulo) großer ganzer Zahlen.

Es sind noch einige Restarbeiten zu erledigen, wie etwa die Betrachtung der unären Operatoren ++ und -- sowie der (expliziten) Konvertierungsoperatoren vom BigInteger-Klassentyp hin zu den elementaren Typen int, long bzw. long long (Listing 13):

01: // increment operator: prefix version
02: BigInteger& operator++ (BigInteger& a)
03: {
04:     a += BigInteger{ 1 };
05:     return a;
06: }
07: 
08: // decrement operator: prefix version
09: BigInteger& operator-- (BigInteger& a)
10: {
11:     a -= BigInteger{ 1 };
12:     return a;
13: }
14: 
15: // increment operator: postfix version
16: BigInteger operator++ (BigInteger& a, int)
17: {
18:     BigInteger tmp{ a };  // construct a copy
19:     ++a;                  // increment number
20:     return tmp;           // return the copy
21: }
22: 
23: // decrement operator: postfix version
24: BigInteger operator-- (BigInteger& a, int)
25: {
26:     BigInteger tmp(a); // construct a copy
27:     --a;               // decrement number
28:     return tmp;        // return the copy
29: }
30: 
31: // type conversion operators
32: BigInteger::operator int() const
33: {
34:     return static_cast<int> (toLongLong());
35: }
36: 
37: BigInteger::operator long() const
38: {
39:     return static_cast<long> (toLongLong());
40: }
41: 
42: BigInteger::operator long long() const
43: {
44:     return static_cast<long long> (toLongLong());
45: }
46: 
47: // private helper method
48: long long BigInteger::toLongLong() const
49: {
50:     long long n = 0;
51:     std::for_each(std::rbegin(m_digits), std::rend(m_digits), [&](digit_t digit) {
52:         n = 10ll * n + (long long) digit;
53:      });
54:     return (m_sign) ? n : -n;
55: }

Listing 13: Explizite Konvertierungsoperatoren, Inkrement- und Dekrement-Operator.

Nicht fehlen sollte die Methode removeLeadingZeros in unseren Betrachtungen. Sie kommt in der Realisierung der diversen Methoden und Operatoren der BigInteger-Klasse häufig zum Einsatz (Listing 14):

01: void BigInteger::removeLeadingZeros()
02: {
03:     // remove trailing zeros, if any ... using STL algorithms
04:     std::reverse_iterator<std::vector<digit_t>::iterator> r_it{ std::find_if(
05:         std::rbegin(m_digits),
06:         std::rend(m_digits),
07:         [](int value) { return value != 0; }
08:     )};
09: 
10:     // vector contains only '0's - save last '0'
11:     if (r_it == std::rend(m_digits)) {
12:         r_it--;
13:     }
14: 
15:     m_digits.erase(r_it.base(), std::end(m_digits));
16: }

Listing 14: Methode removeLeadingZeros der Klasse BigInteger.

Damit sind am Ende der Lösungsbesprechung angekommen. Welchen Nutzen können wir aus der Klasse BigInteger ziehen? Wir demonstrieren als Beispiel die Fakultätfunktion aus der Mathematik, die jeder Zahl das Produkt aller natürlichen Zahlen kleiner und gleich dieser Zahl zuordnet. Als Notation wird der natürlichen Zahl ein Ausrufezeichen „!” nachgestellt, also

n! = 1 * 2 * 3 * … * n

Beim Berechnen der Fakultät stellen wir fest, dass diese, selbst für vergleichsweise kleine Argumente, schnell einen sehr großen Wert annimmt. Wir können das an einer Methode faculty ausprobieren, die wir auf Basis des Datentyps size_t definieren:

size_t BigFaculty::faculty(size_t n)
{
    if (n == 1)
        return 1;
    else
        return n * faculty(n - 1);
}

Mit dieser Methode faculty machen wir die Beobachtung, dass wir nur für Argumente n kleiner-gleich 21 ein korrektes Resultat erhalten:

Faculty of 1: 1
Faculty of 2: 2
Faculty of 3: 6
Faculty of 4: 24
Faculty of 5: 120
Faculty of 6: 720
Faculty of 7: 5040
Faculty of 8: 40320
Faculty of 9: 362880
Faculty of 10: 3628800
Faculty of 11: 39916800
Faculty of 12: 479001600
Faculty of 13: 6227020800
Faculty of 14: 87178291200
Faculty of 15: 1307674368000
Faculty of 16: 20922789888000
Faculty of 17: 355687428096000
Faculty of 18: 6402373705728000
Faculty of 19: 121645100408832000
Faculty of 20: 2432902008176640000
Faculty of 21: 14197454024290336768
Faculty of 22: 17196083355034583040
Faculty of 23: 8128291617894825984
Faculty of 24: 10611558092380307456
Faculty of 25: 7034535277573963776
Faculty of 26: 16877220553537093632
Faculty of 27: 12963097176472289280
Faculty of 28: 12478583540742619136
Faculty of 29: 11390785281054474240
Faculty of 30: 9682165104862298112

Ab dem Argument n = 22 werden die Resultate falsch, wie sich an der stagnierenden Zahl der Ziffern leicht erkennen lässt. Für die Berechnung haben wir die rekursive Formel der Fakultätfunktion verwendet (Abbildung 7), was aber für die Falschheit der Ergebnisse nicht der Grund ist:

Abbildung 7: Rekursive Definition der Fakultätfunktion.

Mit den regulären Sprachmitteln von C++ kommen wir hier nicht korrekt an das Ziel, der Wertebereich des Datentyps size_t lässt einfach keine größeren Zahlen zu. Ersetzen wir in der Methode faculty den Datentyp size_t durch BigInteger, so können wir die Fakultät korrekt für beliebig große Argumente berechnen. Wir greifen die Gelegenheit noch beim Schopfe und definieren die Methode faculty jetzt als so genannte Template Member Methode. Auf diese Weise haben wir eine einzige Implementierung, die sich für Daten des Typs size_t und BigInteger verwenden lässt:

class BigFaculty
{
public:
    template <typename T>
    static T faculty(const T& n)
    {
        if (n == static_cast<T> (1))
            return static_cast<T> (1);
        else
            return n * faculty(n - static_cast<T> (1));
    }
};

Der einzige – wenn wir das so sehen wollen – unschöne Aspekt dieser Realisierung ist die Verwendung von konstanten Werten. Für die Konstante 1 (Datentyp int oder auch size_t) bzw. 1_big (Datentyp BigInteger) schreiben wir in einer generischen Methode static_cast<T>(1) (Datentyp T). Da die Wartung einer Methode in jedem Fall besser ist als die von zwei Methoden, bevorzuge ich diese Variante.

Nebenbei bemerkt ist die aus der Mathematik hinlänglich bekannte Fakultät-Funktion ein guter Kandidat, um vorzugsweise die Subtraktion und Multiplikation intensiv testen zu können. Mit folgendem Testrahmen sehen die ersten fünfunddreißig Fakultäten so aus:

void Test_Faculty(int limit)
{
    for (BigInteger n{ 1 }; n != BigInteger { limit }; ++n)
    {
        BigInteger f{ BigFaculty::faculty(n) };
        std::cout << "Faculty of " << n << ": " << f << std::endl;
    }
}

Ausgabe (für limit gleich 36):

Faculty of 1: 1
Faculty of 2: 2
Faculty of 3: 6
Faculty of 4: 24
Faculty of 5: 120
Faculty of 6: 720
Faculty of 7: 5.040
Faculty of 8: 40.320
Faculty of 9: 362.880
Faculty of 10: 3.628.800
Faculty of 11: 39.916.800
Faculty of 12: 479.001.600
Faculty of 13: 6.227.020.800
Faculty of 14: 87.178.291.200
Faculty of 15: 1.307.674.368.000
Faculty of 16: 20.922.789.888.000
Faculty of 17: 355.687.428.096.000
Faculty of 18: 6.402.373.705.728.000
Faculty of 19: 121.645.100.408.832.000
Faculty of 20: 2.432.902.008.176.640.000
Faculty of 21: 51.090.942.171.709.440.000
Faculty of 22: 1.124.000.727.777.607.680.000
Faculty of 23: 25.852.016.738.884.976.640.000
Faculty of 24: 620.448.401.733.239.439.360.000
Faculty of 25: 15.511.210.043.330.985.984.000.000
Faculty of 26: 403.291.461.126.605.635.584.000.000
Faculty of 27: 10.888.869.450.418.352.160.768.000.000
Faculty of 28: 304.888.344.611.713.860.501.504.000.000
Faculty of 29: 8.841.761.993.739.701.954.543.616.000.000
Faculty of 30: 265.252.859.812.191.058.636.308.480.000.000
Faculty of 31: 8.222.838.654.177.922.817.725.562.880.000.000
Faculty of 32: 263.130.836.933.693.530.167.218.012.160.000.000
Faculty of 33: 8.683.317.618.811.886.495.518.194.401.280.000.000
Faculty of 34: 295.232.799.039.604.140.847.618.609.643.520.000.000
Faculty of 35: 10.333.147.966.386.144.929.666.651.337.523.200.000.000

Die Division sollten wir ebenfalls einem intensiven Test unterziehen. Wir betrachten aus diesem Grund Potenzen der Zahl 2, berechnen diese allerdings nicht beginnend mit der 2, sondern in umgekehrter Richtung. Einen sehr großen Startwert (2.475.880.078.570.760.549.798.248.448) habe ich vorab mit Hilfe der Multiplikations-Methode ausgerechnet:

BigInteger huge{ "2.475.880.078.570.760.549.798.248.448" };

while (huge != 1_big)
{
    std::cout << huge << " / 2 = ";
    huge = huge / 2_big;
    std::cout << huge << std::endl;
}

Ausgabe:

2.475.880.078.570.760.549.798.248.448 / 2 = 1.237.940.039.285.380.274.899.124.224
1.237.940.039.285.380.274.899.124.224 / 2 = 618.970.019.642.690.137.449.562.112
618.970.019.642.690.137.449.562.112 / 2 = 309.485.009.821.345.068.724.781.056
309.485.009.821.345.068.724.781.056 / 2 = 154.742.504.910.672.534.362.390.528
154.742.504.910.672.534.362.390.528 / 2 = 77.371.252.455.336.267.181.195.264
77.371.252.455.336.267.181.195.264 / 2 = 38.685.626.227.668.133.590.597.632
38.685.626.227.668.133.590.597.632 / 2 = 19.342.813.113.834.066.795.298.816
19.342.813.113.834.066.795.298.816 / 2 = 9.671.406.556.917.033.397.649.408
9.671.406.556.917.033.397.649.408 / 2 = 4.835.703.278.458.516.698.824.704
4.835.703.278.458.516.698.824.704 / 2 = 2.417.851.639.229.258.349.412.352
2.417.851.639.229.258.349.412.352 / 2 = 1.208.925.819.614.629.174.706.176
1.208.925.819.614.629.174.706.176 / 2 = 604.462.909.807.314.587.353.088
604.462.909.807.314.587.353.088 / 2 = 302.231.454.903.657.293.676.544
302.231.454.903.657.293.676.544 / 2 = 151.115.727.451.828.646.838.272
151.115.727.451.828.646.838.272 / 2 = 75.557.863.725.914.323.419.136
75.557.863.725.914.323.419.136 / 2 = 37.778.931.862.957.161.709.568
37.778.931.862.957.161.709.568 / 2 = 18.889.465.931.478.580.854.784
18.889.465.931.478.580.854.784 / 2 = 9.444.732.965.739.290.427.392
9.444.732.965.739.290.427.392 / 2 = 4.722.366.482.869.645.213.696
4.722.366.482.869.645.213.696 / 2 = 2.361.183.241.434.822.606.848
2.361.183.241.434.822.606.848 / 2 = 1.180.591.620.717.411.303.424
1.180.591.620.717.411.303.424 / 2 = 590.295.810.358.705.651.712
590.295.810.358.705.651.712 / 2 = 295.147.905.179.352.825.856
295.147.905.179.352.825.856 / 2 = 147.573.952.589.676.412.928
147.573.952.589.676.412.928 / 2 = 73.786.976.294.838.206.464
73.786.976.294.838.206.464 / 2 = 36.893.488.147.419.103.232
36.893.488.147.419.103.232 / 2 = 18.446.744.073.709.551.616
18.446.744.073.709.551.616 / 2 = 9.223.372.036.854.775.808
9.223.372.036.854.775.808 / 2 = 4.611.686.018.427.387.904
4.611.686.018.427.387.904 / 2 = 2.305.843.009.213.693.952
2.305.843.009.213.693.952 / 2 = 1.152.921.504.606.846.976
1.152.921.504.606.846.976 / 2 = 576.460.752.303.423.488
576.460.752.303.423.488 / 2 = 288.230.376.151.711.744
288.230.376.151.711.744 / 2 = 144.115.188.075.855.872
144.115.188.075.855.872 / 2 = 72.057.594.037.927.936
72.057.594.037.927.936 / 2 = 36.028.797.018.963.968
36.028.797.018.963.968 / 2 = 18.014.398.509.481.984
18.014.398.509.481.984 / 2 = 9.007.199.254.740.992
9.007.199.254.740.992 / 2 = 4.503.599.627.370.496
4.503.599.627.370.496 / 2 = 2.251.799.813.685.248
2.251.799.813.685.248 / 2 = 1.125.899.906.842.624
1.125.899.906.842.624 / 2 = 562.949.953.421.312
562.949.953.421.312 / 2 = 281.474.976.710.656
281.474.976.710.656 / 2 = 140.737.488.355.328
140.737.488.355.328 / 2 = 70.368.744.177.664
70.368.744.177.664 / 2 = 35.184.372.088.832
35.184.372.088.832 / 2 = 17.592.186.044.416
17.592.186.044.416 / 2 = 8.796.093.022.208
8.796.093.022.208 / 2 = 4.398.046.511.104
4.398.046.511.104 / 2 = 2.199.023.255.552
2.199.023.255.552 / 2 = 1.099.511.627.776
1.099.511.627.776 / 2 = 549.755.813.888
549.755.813.888 / 2 = 274.877.906.944
274.877.906.944 / 2 = 137.438.953.472
137.438.953.472 / 2 = 68.719.476.736
68.719.476.736 / 2 = 34.359.738.368
34.359.738.368 / 2 = 17.179.869.184
17.179.869.184 / 2 = 8.589.934.592
8.589.934.592 / 2 = 4.294.967.296
4.294.967.296 / 2 = 2.147.483.648
2.147.483.648 / 2 = 1.073.741.824
1.073.741.824 / 2 = 536.870.912
536.870.912 / 2 = 268.435.456
268.435.456 / 2 = 134.217.728
134.217.728 / 2 = 67.108.864
67.108.864 / 2 = 33.554.432
33.554.432 / 2 = 16.777.216
16.777.216 / 2 = 8.388.608
8.388.608 / 2 = 4.194.304
4.194.304 / 2 = 2.097.152
2.097.152 / 2 = 1.048.576
1.048.576 / 2 = 524.288
524.288 / 2 = 262.144
262.144 / 2 = 131.072
131.072 / 2 = 65.536
65.536 / 2 = 32.768
32.768 / 2 = 16.384
16.384 / 2 = 8.192
8.192 / 2 = 4.096
4.096 / 2 = 2.048
2.048 / 2 = 1.024
1.024 / 2 = 512
512 / 2 = 256
256 / 2 = 128
128 / 2 = 64
64 / 2 = 32
32 / 2 = 16
16 / 2 = 8
8 / 2 = 4
4 / 2 = 2
2 / 2 = 1

Zum Abschluss betrachten wir noch Mersenne-Zahlen. Eine Mersenne-Zahl ist eine Zahl der Form 2n - 1. Die Primzahlen unter den Mersenne-Zahlen werden Mersenne-Primzahlen genannt. Diese können wiederum, wie Sie vermuten, sehr groß werden. Im Jahre 1963 gelang es dem Mathematiker Donald B. Gillies nachzuweisen, dass für den Exponenten n = 11213 die resultierende Mersenne-Zahl prim ist. Sollte es mir gelungen sein, Ihr Interesse an Mersenne-Primzahlen zu wecken, dann dürfen Sie zum Abschluss – mit Hilfe der BigInteger-Klasse – einen Blick auf diese Zahl werfen. In der Liste aller bekannten Mersenne-Primzahlen rangiert sie an der 23. Stelle:

BigInteger mersenne { BigMersenne::number(11213) };
std::cout << "Mersenne: " << std::endl;
std::cout << mersenne(16) << std::endl;
std::cout << "Number of Digits: " << mersenne.size() << std::endl;

Beachten Sie in dem Code-Fragment: Zur Ausgabe der Mersenne-Zahl greifen wir auf den Funktor in der Klasse BigInteger zurück. Es sollen pro Zeile 16 Dreiziffernblöcke ausgegeben werden.

Ausgabe:

Mersenne:
2.814.112.013.697.373.133.393.152.975.842.584.191.818.662.382.013.
  600.787.892.419.349.345.515.176.682.276.313.810.715.094.745.633.
  257.074.198.789.308.535.071.537.342.445.016.418.881.801.789.390.
  548.709.414.391.857.257.571.565.758.706.478.418.356.747.070.674.
  633.497.188.053.050.875.416.821.624.325.680.555.826.071.110.691.
  946.607.460.873.056.965.360.830.571.590.242.774.934.226.866.183.
  966.309.185.433.462.514.537.484.258.655.982.386.235.046.029.227.
  507.801.410.907.163.348.439.547.781.093.397.260.096.909.677.091.
  843.944.555.754.221.115.477.343.760.206.979.650.067.087.884.993.
  478.012.977.277.878.532.807.432.236.554.020.931.571.802.310.429.
  923.167.588.432.457.036.104.110.850.960.439.769.038.450.365.514.
  022.349.625.383.665.751.207.169.661.697.352.732.236.111.926.846.
  454.751.701.734.527.011.379.148.175.107.820.821.297.628.946.795.
  631.098.960.767.492.250.494.834.254.073.334.414.121.627.833.939.
  461.539.212.528.932.010.726.136.689.293.688.815.665.491.671.395.
  174.710.452.663.709.175.753.603.774.156.855.766.515.313.827.613.
  727.281.696.692.633.529.666.363.787.286.539.769.941.609.107.777.
  183.593.336.002.680.124.517.633.451.490.439.598.324.823.836.457.
  251.219.406.391.432.635.639.225.604.556.042.396.004.307.799.361.
  927.379.900.586.400.420.763.092.320.813.392.262.492.942.076.312.
  933.268.033.818.471.555.255.820.639.308.889.948.665.570.202.403.
  815.856.313.578.949.779.767.046.261.845.327.956.725.767.289.205.
  262.311.752.014.786.247.813.331.834.015.084.475.386.760.526.612.
  217.340.579.721.237.414.485.803.725.355.463.022.009.536.301.008.
  145.867.524.704.604.618.862.039.093.555.206.195.328.240.951.895.
  107.040.793.284.825.095.462.530.151.872.823.997.171.764.140.663.
  315.804.309.008.611.942.578.380.931.064.748.991.594.407.476.328.
  437.785.848.825.423.921.170.614.938.294.029.483.257.162.979.299.
  388.940.695.877.375.448.948.081.108.345.293.394.327.808.452.729.
  789.834.135.140.193.912.419.661.799.488.795.210.328.238.112.742.
  218.700.634.541.149.743.657.287.232.843.426.369.348.804.878.993.
  471.962.403.393.967.857.676.150.371.600.196.650.252.168.250.117.
  793.178.488.012.000.505.422.821.362.550.520.509.209.724.459.895.
  852.366.827.477.851.619.190.503.254.853.115.029.403.132.178.989.
  005.195.751.194.301.340.277.282.730.390.683.651.120.587.895.060.
  198.753.121.882.187.788.657.024.007.291.784.186.518.589.977.788.
  510.306.743.945.896.108.645.258.766.415.692.825.664.174.470.616.
  153.305.144.852.273.884.549.635.059.255.410.606.458.427.323.864.
  109.506.687.636.314.447.514.269.094.932.953.219.924.212.594.695.
  157.655.009.158.521.173.420.923.275.882.063.327.625.408.617.963.
  032.962.033.572.563.553.604.056.097.832.111.547.535.908.988.433.
  816.919.747.615.817.161.606.620.557.307.000.377.194.730.013.431.
  815.560.750.159.027.842.164.901.422.544.571.224.546.936.793.234.
  970.894.954.668.425.436.412.347.785.376.194.310.030.139.080.568.
  383.420.772.628.618.722.646.109.707.506.566.928.102.800.033.961.
  704.343.991.962.002.059.794.565.527.774.913.883.237.756.792.720.
  065.543.768.640.792.177.441.559.278.272.350.823.092.843.683.534.
  396.679.150.229.676.101.834.243.787.820.420.087.274.028.617.212.
  684.576.388.733.605.769.491.224.109.866.592.577.360.666.241.467.
  280.158.988.605.523.486.345.880.882.227.855.505.706.309.276.349.
  415.034.547.677.180.618.296.352.866.263.005.509.222.254.318.459.
  768.194.126.727.603.047.460.344.175.581.029.298.320.171.226.355.
  234.439.676.816.309.919.127.574.206.334.807.719.021.875.413.891.
  580.871.529.049.187.829.308.412.133.400.910.419.756.313.021.540.
  478.436.604.178.446.757.738.998.632.083.586.207.992.234.085.162.
  634.375.406.771.169.707.323.213.988.284.943.779.122.171.985.953.
  605.897.902.291.781.768.286.548.287.878.180.415.060.635.460.047.
  164.104.095.483.777.201.737.468.873.324.068.550.430.695.826.210.
  304.316.336.385.311.384.093.490.021.332.372.463.463.373.977.427.
  405.896.673.827.544.203.128.574.874.581.960.335.232.005.637.229.
  319.592.369.288.171.375.276.702.260.450.911.735.069.504.025.016.
  667.755.214.932.073.643.654.199.488.477.010.363.909.372.005.757.
  899.989.580.775.775.126.621.113.057.905.717.449.417.222.016.070.
  530.243.916.116.705.990.451.304.256.206.318.289.297.738.303.095.
  152.430.549.772.239.514.964.821.601.838.628.861.446.301.936.017.
  710.546.777.503.109.263.030.994.747.397.618.576.207.373.447.725.
  441.427.135.362.428.360.863.669.327.157.635.983.045.447.971.816.
  718.801.639.869.547.525.146.305.655.571.843.717.916.875.669.140.
  320.724.978.568.586.718.527.586.602.439.602.335.283.513.944.980.
  064.327.030.278.104.224.144.971.883.680.541.689.784.796.267.391.
  476.087.696.392.191
Number of Digits: 3376

There‘s more

Natürlich gibt es noch weitere mathematische Spielereien, für die sich die Klasse BigInteger eignet. Wir geben abschließend zwei Anregungen: Perfekte Zahlen und Primzahlen:

Definition: Eine ganze (positive) Zahl wird perfekte (auch vollkommene) Zahl genannt, wenn sie gleich der Summe aller ihrer (positiven) Teiler außer sich selbst ist.

Die ersten 5 perfekten Zahlen lauten 6, 28, 496, 8.128 und 33.550.336.

Weitaus bekannter dürfte die Definition für Primzahlen sein:

Definition: Eine Primzahl ist eine ganze (positive) Zahl, die größer als 1 und ausschließlich durch sich selbst und durch 1 teilbar ist.

Sowohl perfekte Zahlen als auch Primzahlen lassen sich mit den herkömmlichen Sprachmitteln von C++ (und natürlich auch anderen Hochsprachen) relativ einfach bestimmen – wenn wir nur auf der Suche nach vergleichsweise „kleinen” Zahlen sind. Für die Bestimmung größerer Zahlen benötigen wir Hilfsmittel wie beispielsweise die Klasse BigInteger. Um es vorweg zu nehmen: Wir werden mit einem zweiten Problem konfrontiert sein: Der Laufzeit des jeweiligen Programms. Wie lange derartige Berechnungen sein können, dürfen Sie mit folgendem Code-Fragment eruieren. Die beteiligten Klassen BigPerfectNumbers und BigPrimeNumbers finden Sie hier vor. Die Berechnung der ersten drei perfekten Zahlen mit der Klasse BigInteger fällt bzgl. ihrer Laufzeit noch nicht so sehr ins Gewicht:

std::chrono::system_clock::time_point begin{ std::chrono::system_clock::now() };

BigInteger limit{ 500 };
for (BigInteger n{ 2 }; n != limit; ++n) {
    if (BigPerfectNumbers::isPerfect(n)) {
        std::cout << n << " is *perfect*" << std::endl;
    }
}

std::chrono::system_clock::time_point end{ std::chrono::system_clock::now() };
std::chrono::system_clock::duration duration{ end - begin };
double ticks{ std::chrono::duration<double>(duration).count() };
std::cout << ticks << " seconds." << std::endl;

Ausgabe:

6 is *perfect*
28 is *perfect*
496 is *perfect*
0.144654 seconds.

Allerdings sollte nicht verschwiegen werden, dass ich zur Ausführung des Programms den Release-Modus gewählt habe. Spannender wird es mit dem nächsten Code-Fragment: Hier habe ich aus Wikipedia die ersten 10 perfekten Zahlen übernommen. Die Aufgabe des Code-Fragments besteht gewissermaßen darin, eine Überprüfung der Angaben aus Wikipedia zu machen – wenngleich ich natürlich nicht den geringsten Zweifel an der Korrektheit habe. Um es gleich vorweg zu nehmen: Auf meinem Rechner habe ich das Ende der Berechnungen nicht abgewartet … Vielleicht schaffen Sie es auf Ihrem Rechner – und möglicherweise mit adäquaten Optimierungen an der BigInteger-Klasse – das Ziel zu erreichen?

std::chrono::system_clock::time_point begin{ std::chrono::system_clock::now() };

// https://en.wikipedia.org/wiki/List_of_perfect_numbers
std::vector<BigInteger> candidates
{
    6_big,
    28_big,
    496_big,
    8'128_big,
    33'550'336_big,
    8'589'869'056_big,
    137'438'691'328_big,
    2'305'843'008'139'952'128_big,
    2'658'455'991'569'831'744'654'692'615'953'842'176_big,
    191'561'942'608'236'107'294'793'378'084'303'638'130'997'321'548'169'216_big
};

std::for_each(std::begin(candidates), std::end(candidates), [](const BigInteger& candidate) {
    if (BigPerfectNumbers::isPerfect(candidate)) {
        std::cout << candidate << " is *perfect*" << std::endl;
    }
});

std::chrono::system_clock::time_point end{ std::chrono::system_clock::now() };
std::chrono::system_clock::duration duration{ end - begin };
double ticks{ std::chrono::duration<double>(duration).count() };
std::cout << ticks << " seconds." << std::endl;

Auch die Suche nach sehr großen Primzahlen ist ein beliebtes Steckenpferd von Mathematikern. Eine sehr einfache, leider auch sehr laufzeitintensive Methode zur Überprüfung der Primzahleigenschaft einer BigInteger-Zahl sieht so aus:

bool BigPrimeNumbers::isPrime(const BigInteger& number)
{
    // the smallest prime number is 2
    if (number <= 2_big)
        return number == 2_big;

    // even numbers other than 2 are not prime
    if (number % 2_big == 0_big)
        return false;

    // check odd divisors from 3 to the half of the number
    // (in lack of a high precision sqare root function) 
    BigInteger end = number / 2_big + 1_big;
    for (BigInteger i{ 3 }; i <= end; i += 2_big) {
        BigInteger tmp{ number % i };
        if (tmp.zero())
            return false;
    }

    // found prime number
    return true;
}

Mit dieser Funktion isPrime kann man prinzipiell jeden beliebigen Bereich von Zahlen nach Primzahlen durchforsten, zum Beispiel auf diese Weise:

    BigInteger lower{ 10000 };
    BigInteger upper{ 11001 };
    BigInteger count{};

    for (BigInteger i{ lower }; i != upper; ++i)
    {
        if (BigPrimeNumbers::isPrime(i)) {
            std::cout << "  found " << i << std::endl;
            count++;
        }
    }

    std::cout 
        << count << " prime numbers between " << lower << " and " 
        << (upper - 1_big) << "." << std::endl;

Eng verbunden mit der Primzahleigenschaft einer natürlichen Zahl ist auch die Fragestellung, aus welchen Primfaktoren eine natürliche Zahl besteht. Dazu stellen wir die folgende Methode hasPrimeFactor bereit:

std::pair<BigInteger, BigInteger> BigPrimeNumbers::hasPrimeFactor(const BigInteger& number)
{
    // std::pair<BigInteger, BigInteger> result{ 1_big , number };
    std::pair<BigInteger, BigInteger> result{ (BigInteger) 1 , number };

    // factorizing a big integer object using a very simple approach
    for (BigInteger i{ 2 }; i != number; ++i)
    {
        BigInteger tmp{ number % i };
        if (tmp.zero())
        {
            result.first = i;
            result.second = number / i;
            break;
        }
    }

    return result;
}

hasPrimeFactor ermittelt zunächst nicht alle Primfaktoren einer Zahl, sondern bricht die Suche nach dem ersten gefundenen Primfaktor ab. Im Resultat-std::pair<>-Objekt befindet sich im ersten Eintrag eine 1, wenn die Zahl prim ist, anderfalls ist in first ein Primfaktor abgelegt (second enthält den Rest bei Division mit dem gefundenen Primfaktor). Ein Testszenario könnte so aussehen:

std::chrono::system_clock::time_point begin{ std::chrono::system_clock::now() };

BigInteger number{ 13821503_big * 13821503_big };

std::pair<BigInteger, BigInteger> result{ BigPrimeNumbers::hasPrimeFactor(number) };

if (result.first != 1_big)
{
    std::cout
        << "Found factors " << result.first << " and "
        << result.second << "." << std::endl;
}
else
{
    std::cout << number << " is prime." << std::endl;
}

std::chrono::system_clock::time_point end{ std::chrono::system_clock::now() };
std::chrono::system_clock::duration duration{ end - begin };
double ticks{ std::chrono::duration<double>(duration).count() };
std::cout << ticks << " seconds." << std::endl;

Ausgabe:

Found factors 13.821.503 and 13.821.503.
220.308 seconds.

Okay, das Ergebnis stimmt, die Laufzeit des Programms ist allerdings doch unangenehm lang, um es vornehm auszudrücken. Zu Primzahlen – und auch zu anderen mathematischen Spielereien – ließen sich noch unendlich viele Beispiele finden. Wir wollen dieses Thema mit einer Funktion getPrimeFactors abschließen, die zu einer natürliche Zahl alle ihre Primfaktoren berechnet:

std::vector<BigInteger> BigPrimeNumbers::getPrimeFactors(BigInteger number)
{
    std::vector<BigInteger> factors;
    BigInteger factor{ 2 };

    while (number != 1_big)
    {
        if (number % factor == 0_big)
        {
            // store found factor in result vector
            factors.push_back(factor);

            // divide number through this prime factor
            number = number / factor;

            // remove same prime factor, if any
            while (number % factor == 0_big) {
                number = number / factor;
            }
        }

        factor++;
    }

    return factors;
}

Auch hierzu ein Beispiel:

// testing getPrimeFactors
BigInteger candidate{ 44100_big };  // 44100 = 2 * 2 * 3 * 3 * 5 * 5 * 7 * 7

std::vector<BigInteger> factors{ BigPrimeNumbers::getPrimeFactors(candidate) };

std::cout << "Prime factorization of " << candidate << ':' << std::endl;
std::for_each(std::begin(factors), std::end(factors), [](const BigInteger& factor) {
    std::cout << "  found factor " << factor << std::endl;
    });
std::cout << "Done." << std::endl;

Ausgabe:

Prime factorization of 44.100:
  found factor 2
  found factor 3
  found factor 5
  found factor 7
Done.

Cpp_11 Cpp_17 Core

Exakte Arithmetik ganzer Zahlen

Lernziele

Grundgerüst der Klasse `BigInteger`

Ausgabe

Arithmetische Operatoren der Klasse `BigInteger`

Vergleichsoperatoren der Klasse `BigInteger`

Hilfsmethoden der Klasse `BigInteger`

Einige Beispiele

Lösung

There‘s more

See also

Lernziele

Grundgerüst der Klasse BigInteger

Ausgabe

Arithmetische Operatoren der Klasse BigInteger

Vergleichsoperatoren der Klasse BigInteger

Hilfsmethoden der Klasse BigInteger

Einige Beispiele

Lösung

There‘s more

See also

Grundgerüst der Klasse `BigInteger`

Arithmetische Operatoren der Klasse `BigInteger`

Vergleichsoperatoren der Klasse `BigInteger`

Hilfsmethoden der Klasse `BigInteger`