Unter dem Gray-Code versteht man eine Folge binärer Zahlenketten, die nach dem Ingenieur Frank Gray, einem Forscher in den Bell Laboratories, benannt wurde. Er erhielt im Jahre 1953 für die Nutzung des nach ihm benannten Codes das U.S. Patent No. 2 632 058 „Pulse Code Communication”. Durch die Anzahl der Bits wird die Länge n eines Gray-Codes festgelegt. Man kann sich leicht überlegen, dass es zu einem bestimmten n 2n unterschiedliche Gray-Codes gibt.
Wir benutzen die Gray-Code-Darstellung, um an Hand einer Reihe von C++–Klassen das Zusammenspiel unterschiedlicher C++–Sprachkonstrukte zu üben und zu vertiefen. Das Endergebnis dieser Aufgabe, die Berechnung von Gray-Codes zu einem beliebigen n, ließe sich sicherlich auch kürzer und direkter erzielen, nur würden wir dabei keinen Lerneffekt erreichen.
Lernziele
- Container
std::list<T> - Algorithmen
std::for_each,std::begin,std::end,std::rbeginundstd::rend - Lambda-Funktionen mit Zugriffsklausel
- Initialisierungsliste
- Bereichsbasierte
for-Wiederholungsschleife (Range-basedfor-Loop)
Einführung
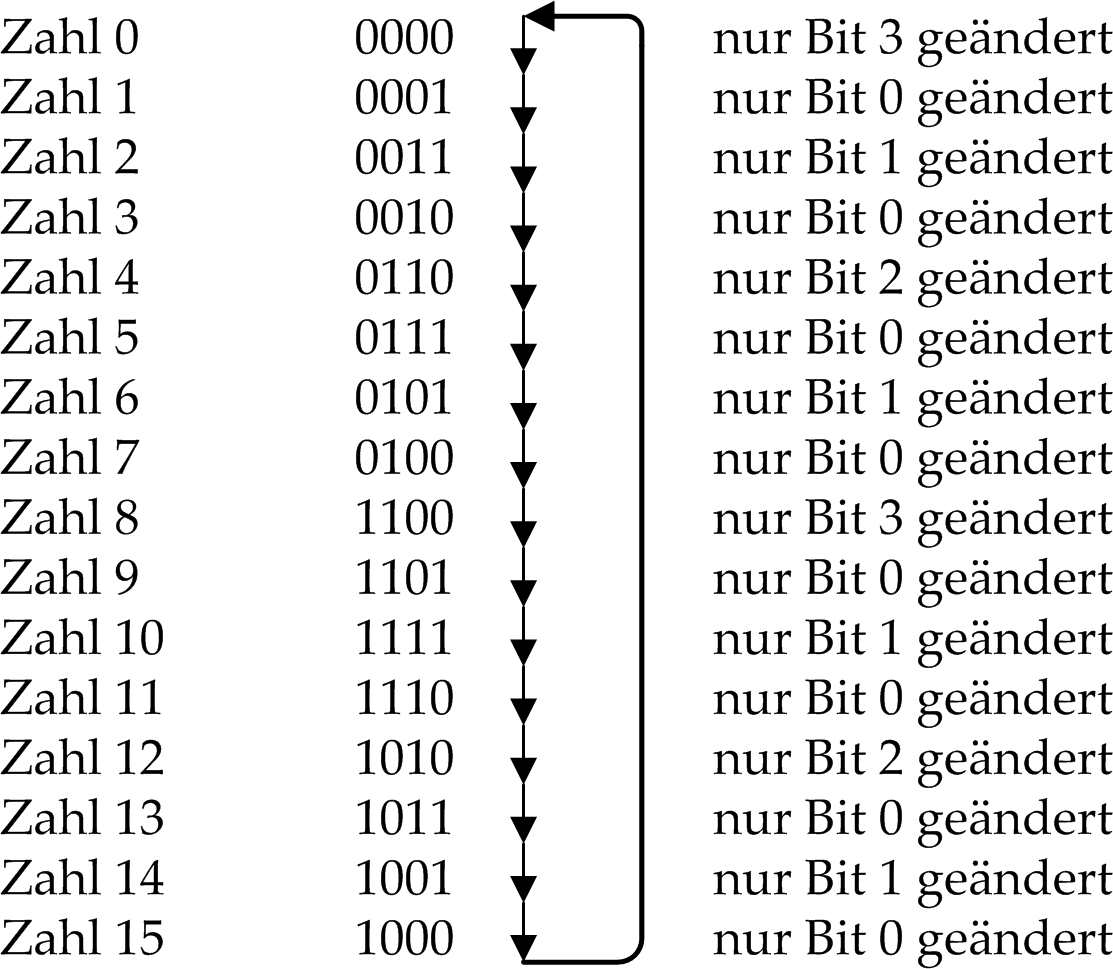
Die Besonderheit des Gray-Codes liegt darin, dass sich benachbarte Zahlenketten nur in genau einem Bit unterscheiden. Dies gilt auch für den Übergang vom 2n-1.-ten Code zum 0.-ten Code:
Definition: Eine Folge aller 2n Bitketten der Länge n (n ≥ 1) heißt ein Gray-Code der Länge n, falls sich jeweils 2 benachbarte Bitketten in nur einer Bitposition unterscheiden.
Diese Eigenschaft kommt vielen Anwendungen zu Gute, wie wir beispielsweise an einem Inkrementalgeber erörtern können.
Würde ein Inkrementalgeber eine herkömmliche Binärzahl (im Zweier-Komplement) als Position liefern,
also etwa 0101 für 5 und 0110 für 6, dann gäbe es ein Problem,
wenn nicht alle Bits absolut gleichzeitig ihre Wertigkeit ändern.
In diesem Fall könnten „Phantomwerte” wie 0100 (4) oder 0111 (7) auftreten.
Der Gray-Code hat dieses Problem nicht, da sich benachbarte Werte nur in einem Bit unterscheiden.
In Abbildung 1 wird diese Eigenschaft am Beispiel des 4-Bit-Gray-Codes demonstriert:
Abbildung 1: 4-Bit-Gray-Code.
Erzeugung von Gray-Codes
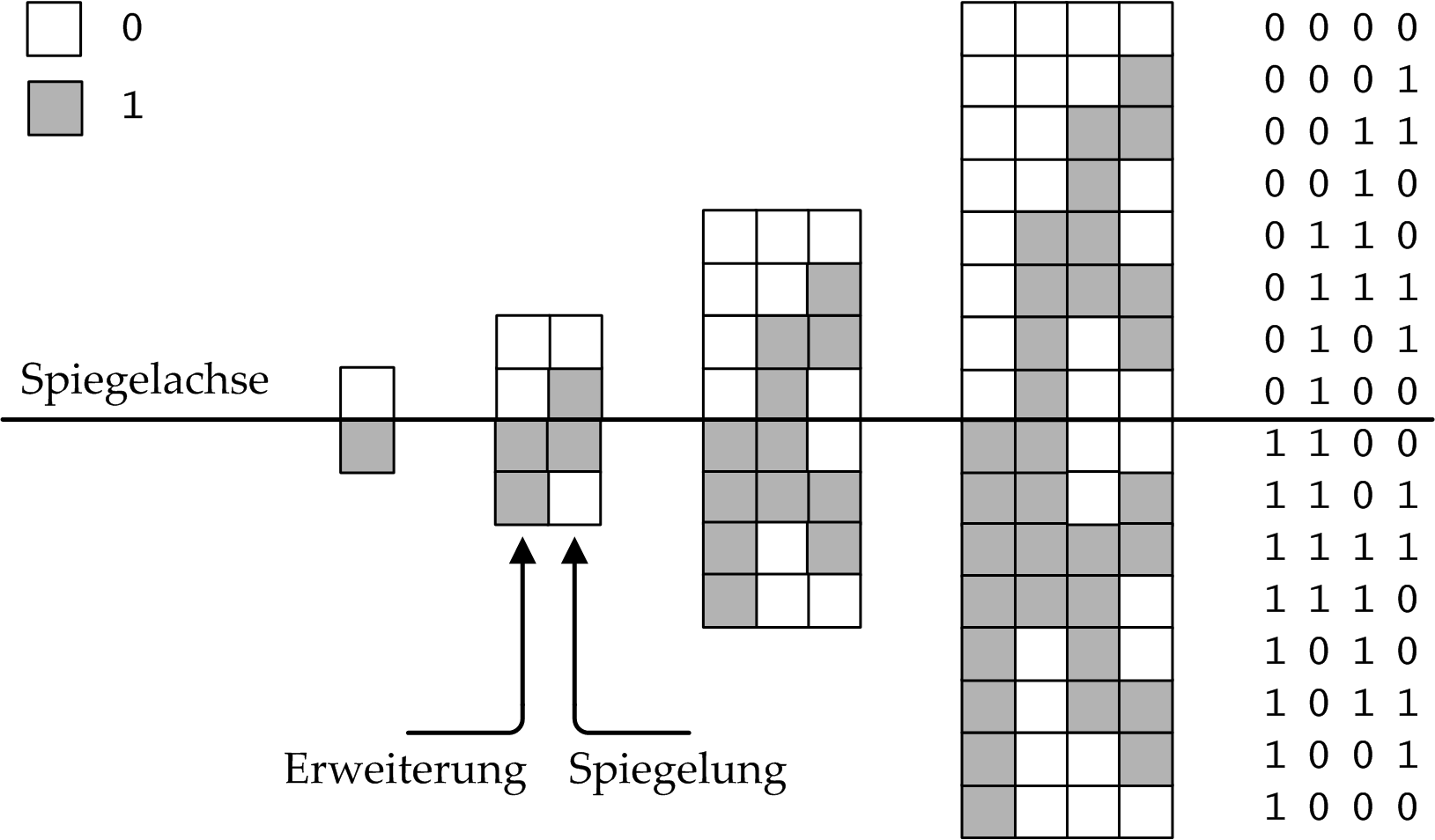
Um Gray-Codes einer bestimmten Länge zu erzeugen, ist eine Darstellung wie in Abbildung 2 gezeigt intuitiver. Ausgehend von einer Kombination der beiden Bits 0 und 1 wird durch wiederholtes Spiegeln der Ausgangsinformation und Hinzufügen von 0- und 1-Werten an der höchstwertigen Stelle der vollständige Gray-Code aufgebaut. In Abbildung 2 finden Sie die sukzessive Erzeugung des 1-, 2- und 3-Bit-Gray-Codes bis hin zum 4-Bit-Gray-Code vor:
Abbildung 2: Bildung des Gray-Codes durch Spiegelung und Bitergänzung.
Erstellen Sie eine „Modern C++”–Anwendung, die möglichst einfallsreich alle Gray-Codes für ein beliebiges n berechnet. Orientieren Sie sich in Ihrer Realisierung an den Details von Tabelle 1:
| Element | Beschreibung |
|---|---|
Methode calculate |
static std::list<std::list<bool>> calculate(size_t len);.Berechnet alle Gray-Codes einer bestimmten Länge len. Das Ergebnis wird in einem std::list<std::list<bool>>-Objekt zusammengestellt. |
Tabelle 1: Wesentliche Elemente der Klasse GrayCodeCalculator.
Lösung
Quellcode: Siehe auch Github.
Wir beginnen mit einigen Vorüberlegungen zur Repräsentation von Gray-Codes in einem C++–Programm.
Für die Darstellung eines einzelnen Gray-Codes (einer bestimmten Länge) setzen wir die Klasse std::list<bool> ein.
Mehrere Gray-Codes, also std::list<bool>-Objekte, legen wir in einem std::list<std::list<bool>>-Objekt ab.
Damit sind wir schon bei der Klasse GrayCodeCalculator angekommen: Mit Hilfe der calculate-Methode
berechnen wir die Gray-Codes einer bestimmten Länge.
Das Resultat wird in Gestalt eines std::list<std::list<bool>>-Objekts zurückgegeben.
Die calculate-Methode des Kalkulators arbeitet auf einem rekursiven Prinzip.
Liegen für eine bestimmte Länge n alle Gray-Codes vor, so erhält man die Gray-Codes der Länge n+1 wie in Abbildung 2 skizziert wird.
Es werden alle vorliegenden Gray-Codes der Länge n an einer fiktiven Spiegelachse gespiegelt.
Um Gray-Codes der Länge n+1 zu erhalten, werden diese zunächst um ein Bit vorne verlängert (Wert 0 bzw. false).
In einem zweiten Schritt wird dann bei den gespiegelten Gray-Codes an der höchstwertigen Stelle
das Bit auf den Wert 1 (bzw. true) gesetzt. Auf diese Weise lassen sich rekursiv alle Gray-Codes einer bestimmten Länge berechnen.
Damit sind wir schon bei der Implementierung angelangt (Listing 1 und Listing 2):
01: class GrayCodeCalculator
02: {
03: public:
04: // c'tors
05: GrayCodeCalculator() = delete;
06:
07: // public interface
08: static std::list<std::list<bool>> calculate(size_t);
09: static void print(std::list<std::list<bool>>);
10:
11: private:
12: static std::list<std::list<bool>> calculateRankOne();
13: };
Listing 1: Klasse GrayCodeCalculator: Definition.
01: std::list<std::list<bool>> GrayCodeCalculator::calculate(size_t length)
02: {
03: if (length == 0) {
04: throw std::invalid_argument("illegal length argument");
05: }
06: else if (length == 1) {
07: return calculateRankOne();
08: }
09: else {
10: std::list<std::list<bool>> tmp{ calculate(length - 1) };
11:
12: // need a new Gray Code list
13: std::list<std::list<bool>> result;
14:
15: // copy old entries and extend them with 'false'
16: std::for_each(
17: std::begin(tmp),
18: std::end(tmp),
19: [&](const std::list<bool>& v) {
20: std::list<bool> ex{ v };
21: ex.push_front(false);
22: result.push_back(ex);
23: }
24: );
25:
26: // mirror old entries and extend them with 'true'
27: std::for_each(
28: std::rbegin(tmp),
29: std::rend(tmp),
30: [&](const std::list<bool>& v) {
31: std::list<bool> ex{ v };
32: ex.push_front(true);
33: result.push_back(ex);
34: }
35: );
36:
37: return result;
38: }
39: }
40:
41: std::list<std::list<bool>> GrayCodeCalculator::calculateRankOne()
42: {
43: return { { false } , { true } };
44: }
45:
46: void GrayCodeCalculator::print(std::list<std::list<bool>> result)
47: {
48: for (std::list<bool> code : result) {
49: for (bool bit : code) {
50: std::cout << bit;
51: }
52: std::cout << std::endl;
53: }
54: }
Listing 2: Klasse GrayCodeCalculator: Implementierung.
Das Traversieren von C++–Containern wird in Listing 2 auf vielfältige Weise demonstriert.
Da wäre zum einen der std::for_each-Algorithmus (Zeilen 16 und 27). Seine Stärke liegt in der Spezifikation des
zu Grunde liegenden Bereichs. Mit std::begin und std::end wird ein Bereich ganz klassisch vom ersten bis zum letzten Element durchlaufen.
Man kann einen Bereich aber auch in der umgekehrten Reihenfolge durchlaufen, indem man diesen mit std::rbegin und std::rend spezifiziert.
Ein zweite Variation in der Traversierung eines Containers ist die bereichsbasierte for-Wiederholungsschleife.
Sie kommt in den Zeilen 48 und 49 gleich zwei Mal zur Ausgabe des Ergebnisses zum Einsatz.
Interessant in Listing 2 ist auch Zeile 43: Hier finden Sie die Vorbelegung eines std::list<std::list<bool>>-Objekts
mit einer Initialisierungs-Liste vor.
Nun können wir ein GrayCodeCalculator-Objekt bei der Arbeit betrachten.
Wir berechnen zu diesem Zweck alle Gray-Codes bis zur Länge 5:
// testing 1-Bit-Gray-Codes
std::list<std::list<bool>> codes = GrayCodeCalculator::calculate(1);
std::cout << codes.size() << " 1-Bit-Gray-Codes found:" << std::endl;
GrayCodeCalculator::print(codes);
std::cout << std::endl;
// testing 2-Bit-Gray-Codes
codes = GrayCodeCalculator::calculate(2);
std::cout << codes.size() << " 2-Bit-Gray-Codes found:" << std::endl;
GrayCodeCalculator::print(codes);
std::cout << std::endl;
// testing 3-Bit-Gray-Codes
codes = GrayCodeCalculator::calculate(3);
std::cout << codes.size() << " 3-Bit-Gray-Codes found:" << std::endl;
GrayCodeCalculator::print(codes);
std::cout << std::endl;
// testing 4-Bit-Gray-Codes
codes = GrayCodeCalculator::calculate(4);
std::cout << codes.size() << " 4-Bit-Gray-Codes found:" << std::endl;
GrayCodeCalculator::print(codes);
std::cout << std::endl;
// testing 5-Bit-Gray-Codes
codes = GrayCodeCalculator::calculate(5);
std::cout << codes.size() << " 5-Bit-Gray-Codes found:" << std::endl;
GrayCodeCalculator::print(codes);
Ausgabe:
2 1-Bit-Gray-Codes found:
0
1
4 2-Bit-Gray-Codes found:
00
01
11
10
8 3-Bit-Gray-Codes found:
000
001
011
010
110
111
101
100
16 4-Bit-Gray-Codes found:
0000
0001
0011
0010
0110
0111
0101
0100
1100
1101
1111
1110
1010
1011
1001
1000
32 5-Bit-Gray-Codes found:
00000
00001
00011
00010
00110
00111
00101
00100
01100
01101
01111
01110
01010
01011
01001
01000
11000
11001
11011
11010
11110
11111
11101
11100
10100
10101
10111
10110
10010
10011
10001
10000
There‘s more
Gray-Codes lassen sich sowohl mit einem rekursiven als auch mit einem iterativen Algorithmus berechnen. Versuchen Sie, an Hand der Beschreibung des Algorithmus in Abbildung 2 eine iterative Realisierung in C++ umzusetzen. Die folgende Anregung könnte hierbei behilflich sein.