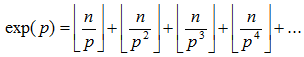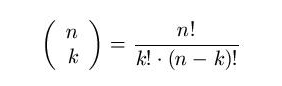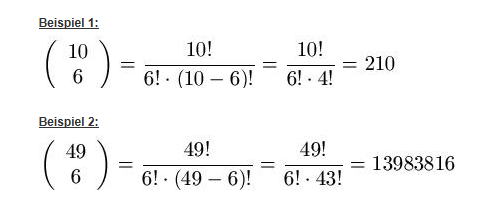Die Fakultät ist in der Mathematik eine Funktion, die einer natürlichen Zahl n das Produkt aller natürlichen Zahlen kleiner und gleich dieser Zahl zuordnet: n! = 1 * 2 * 3 * … * n. In der Kombinatorik spielt die Fakultät ebenfalls eine große Rolle, weil n! die Anzahl der Möglichkeiten ist, unterschiedliche Gegenstände der Reihe nach anzuordnen. Bei diesen Überlegungen kommen auch Binomialkoeffizienten ins Spiel. Sie geben an, auf wie viele verschiedene Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann.
Sowohl Fakultäten als auch Binomialkoeffizienten weisen eine unangenehme Eigenschaft auf:
Ihre Werte können sehr schnell sehr groß werden – und sind damit in Variablen des Typs long oder size_t
nicht mehr darstellbar. Ein Satz von Legendre verschafft hier Abhilfe:
Er befasst sich mit der Frage, wie oft ein Primfaktor in der Primfaktorzerlegung von n! für ein n ∈ N vorkommt –
um damit eine alternative Darstellung für Fakultäten und Binomialkoeffizienten zu ermöglichen, die das Problem des Überlaufs umgehen kann.
Wir betrachten in dieser Fallstudie die Berechnung von Fakultäten und Binomialkoeffizienten sowohl in ihrer klassischen Definition als auch mit Hilfe des Satzes von Legendre als Produkt von Primfaktorzerlegungen.
Lernziele
- Klasse
std::unordered_map - Structured Binding
- Bereichsbasierte
for-Wiederholungsschleife (Range-basedfor-Loop)
Einführung
Notiert wird die Fakultätsfunktion durch ein dem Argument nachgestelltes Ausrufezeichen, einer Schreibweise, die dem elsässischen Mathematiker Christian Kramp (1760 – 1826) zugeordnet wird. Betrachten wir zur Veranschaulichung dieser Funktion beispielsweise die drei Farben Rot, Grün und Blau. Wie viele Möglichkeiten gibt es, sie anzuordnen? Für die erste Position kommen alle drei Farben in Betracht. Ist die erste Farbe gesetzt, können nur noch zwei Farben um die zweite Position konkurrieren. Für die Belegung der Positionen 1 und 2 ergeben sich bei drei Farben also 3 * 2 Möglichkeiten. Für die letzte Position bleibt nur noch eine Farbe übrig, letztlich gilt für die Anzahl der Anordnungsmöglichkeiten somit 3 * 2 * 1 = 3! = 6.
Auch für Binomialkoeffizienten wollen wir ein Beispiel geben. Wie groß ist also die Wahrscheinlichkeit, 6 Richtige aus 49 Möglichkeiten zu raten? Also in anderen Worten: Wie groß ist die Wahrscheinlichkeit eines Lottogewinns? Zur Antwort dieser Frage benötigen wir die Anzahl der verschiedenen Möglichkeiten, 6 Zahlen aus 49 möglichen zu wählen. Dazu müssen wir den Binomialkoeffizienten „49 über 6” berechnen, das Ergebnis ist 13.983.816.
Klasse Factorial
Die Fakultätsfunktion lässt sich sehr einfach iterativ wie auch rekursiv programmieren.
Erstellen Sie eine Klasse Factorial mit zwei Methoden
factorialRecursive und factorialIterative. Die folgenden Code-Fragmente
sollten mit Hilfe Ihrer Implementierung ausführbar sein:
Factorial f(5);
f.factorialIterative();
std::cout << f.get() << "! = " << f.value() << std::endl;
f.set(10);
f.factorialRecursive();
std::cout << f.get() << "! = " << f.value() << std::endl;
Ausgabe:
5! = 120
10! = 3628800
Kontrollfrage: Ab welchem größeren n erhalten Sie mit Ihrem Testprogramm – offensichtlich – falsche Resultate? Welche Erklärung haben Sie dafür?
Nachschlagewerke
Zur Vorbereitung der nachfolgenden Teilaufgaben betrachten wir nun Nachschlagewerke in der Programmierung. Darunter verstehen wir eine Datenstruktur, die zu einer bestimmten Information (auch Schlüssel genannt) einen Wert verwaltet. Ein Telefonbuch ist ein solches Beispiel: Als Schlüssel fungiert ein Name, die Telefonnummer ist ihm als Wert zugeordnet. Fremdsprachenlexika sind ein weiteres Beispiel.
Wozu benötigen wir in dieser Fallstudie Nachschlagewerke?
Im Folgenden zerlegen wir bestimmte Zahlen in ihre Primfaktoren. Als Schlüssel fungiert die
Primzahl, der zugeordnete Wert ist der Exponent, der angibt, wie oft die Primzahl in der zu
zerlegenden Zahl vorkommt. Auf die Primfaktorenzerlegung gehen wir später ein, zunächst
halten wir fest, dass wir eine Klasse PrimeDictionary entwickeln, deren Schlüssel und
Werte jeweils vom Typ size_t sind. Weitere Hinweise entnehmen Sie bitte Tabelle 1:
| Element | Beschreibung |
|---|---|
| Konstruktor | PrimeDictionary();Standardkonstruktor für ein PrimeDictionary-Objekt. |
Methode get |
size_t get(size_t key) const;Liefert Wert zum Schlüssel key zurück. |
Methode set |
void set(size_t key, size_t value);Fügt einen neuen Eintrag (Schlüssel key mit Wert value) in das PrimeDictionary-Objekt ein. |
| Ausgabe | std::ostream& operator<< (std::ostream&, const PrimeDictionary&);Es ist der Standardausgabeoperator zu implementieren. Eine Ausgabe könnte so aussehen: (2,4)(3,2)(5,1)(7,1) |
Tabelle 1: Element der Klasse PrimeDictionary.
Hinweis:
Zur Realisierung der Klasse PrimeDictionary sollten Sie einen geeigneten Container aus der STL einsetzen.
Welche Klasse bietet sich hier an?
Folgendes Code-Fragment sollte mit Hilfe Ihrer Realisierung ausführbar sein:
PrimeDictionary dict{};
dict.set(2, 4); // 2 hoch 4
dict.set(3, 2); // 3 hoch 2
dict.set(5, 0); // 5 hoch 0
dict.set(7, 1); // 7 hoch 1
std::cout << dict << std::endl;
size_t key = 3;
size_t value = dict.get(key);
std::cout << "Value at " << key << ": " << value << std::endl;
dict.set(key, 22);
value = dict.get(key);
std::cout << "Value at " << key << ": " << value << std::endl;
Ausgabe:
(2,4)(3,2)(5,0)(7,1)
Value at 3: 2
Value at 3: 22
Der Satz von Legendre
Die bislang vorgestellten Möglichkeiten zur Berechung der Fakultätsfunktion lösen nicht das
Problem, dass die Werte sehr schnell wachsen und in Variablen des Typs size_t ab einer
bestimmten Größe nicht mehr darstellbar sind. Am Beispiel von
100! =
93.326.215.443.944.152.681.699.238.856.266.700.490.715.968.264.381.621.
468.592.963.895.217.599.993.229.915.608.941.463.976.156.518.286.253.697.
920.827.223.758.251.185.210.916.864.000.000.000.000.000.000.000.000
können Sie das Problem eindrucksvoll erkennen.
Wir kommen nun zu einer anderen Alternative, große Zahlen darzustellen. Speziell für Fakultäten ist dies auf eine Entdeckung des franz. Mathematikers Adrien-Marie Legendre (1752 bis 1833) zurückzuführen. Anstatt die Zahl im Zehnersystem hinzuschreiben, stellen wir sie in ihrer Primfaktorzerlegung dar. Um die Primfaktoren einer Zahl zu berechnen, müssten wir die Zahl aber selbst kennen, werden Sie nun vermutlich argumentieren – wir können sie auf Grund ihrer Größe aber gar nicht softwaretechnisch darstellen. An dieser Stelle kommt nun der Satz von Legendre ins Spiel, er lautet:
Satz von Legendre: In der Primfaktorzerlegung von n! gilt für den Exponenten einer jeder Primzahl, die n! teilt:
Abbildung 1: Der Satz von Legendre mit Gaußklammern.
Hierbei repräsentieren in Abbildung 1 die senkrechten Klammern so genannte „Gaußklammern”: Sie stehen für „die größte ganze Zahl kleiner gleich n/p” am Beispiel des Bruchs n/p. Ferner beachte man: Von den Summanden |n/pi| sind nur endlich viele ungleich 0, nämlich die für alle i mit pi ≤ n.
Beispiel: Wir probieren die Formel am Beispiel von 10! aus. Die 2 hat in der Primfaktorzerlegung von 10! den Exponenten
e(2) = |10/2| + |10/4| + |10/8| = 5 + 2 + 1 = 8.
Für die 3 ergibt sich folgender Exponent:
e(3) = |10/3| + |10/9| = 3 + 1 = 4.
Für 5 gilt:
e(5) = |10/5| = 2.
Damit bleibt nur noch die Primzahl 7 übrig, alle weiteren Primzahlen sind größer als 10:
e(7) = |10/7| = 1.
Wir können uns nun von der Korrektheit des Satzes von Legendre überzeugen. Für die Zahl 10! schreiben wir in der dezimalen Darstellung 3.628.800. Unter Verwendung der Primfaktoren 2, 3, 5, und 7 gilt
28 * 34 * 52 * 71 = 256 * 81 * 25 * 7 = 3.628.800.
Wir sehen, dass bei dieser Darstellung der Wert von n! nicht benötigt wird, die einzelnen Primfaktoren lassen sich nur unter Zuhilfenahme von n berechnen! Da die Hochstellung von Zahlen in einer Konsolenanwendung nicht ganz so einfach ist, modifizieren wir diese Darstellung softwaregerechter ab in
10! = (2,8) (3,4) (5,2) (7,1)
Erweitern Sie nun die Klasse Factorial um eine Methode factorialLegendre, um die
Berechnung der Fakultät einer natürlichen Zahl in Partialbruchzerlegung durchzuführen:
PrimeDictionary factorialLegendre ();
Einen Pseudo-Code für den Satz von Legendre finden Sie in Abbildung 2 vor:
Abbildung 2: Satz von Legendre in Pseudo-Code Darstellung.
Folgendes Code-Fragment sollte damit ausführbar sein:
Factorial f(10);
PrimeDictionary primes = f.factorialLegendre();
std::cout << primes << std::endl;
Ausgabe:
(2,8)(3,4)(5,2)(7,1)
Mit Hilfe des Satzes von Legendre lassen sich weitere Fragen aus der Zahlentheorie beantworten. Ein Beispiel gefällig? Auf wie viele Nullen endet die Zahl 2022! ?
Hinweis: Eine Null am Ende bedeutet, dass die Zahl durch 10 teilbar ist. Wie oft ist 2022! durch 10 teilbar? Sie ist so oft durch 10 teilbar, wie in der Primfaktorzerlegung genügend Zweien und Fünfen vorkommen, um den Faktor 10 zu bilden.
Da der Faktor 2 alle geraden Zahlen teilt und somit häufiger vorhanden ist, lässt sich festhalten, dass die Antwort allein durch die Anzahl der Fünfen bestimmt ist.
Binomialkoeffizienten
Eine weitere Funktion aus dem Themenkreis der Kombinatorik ist der Binomialkoeffizient. Er gibt an, auf wie viele verschiedene Arten man k Objekte aus einer Menge von n verschiedenen Objekten auswählen kann – ohne Zurücklegen und ohne Beachtung der Reihenfolge. Die mathematische Formel zur Berechnung des Binomialkoeffizienten für 0 ≤ n und 0 ≤ k ≤ n lautet wie folgt (Abbildung 3):
Abbildung 3: Definition eines Binomialkoeffizienten.
Auf der linken Seite steht die Kurzschreibweise des Binomialkoeffizienten, gesprochen „n über k”. Auf der rechten Seite steht die Berechnung des Koeffizienten als Bruch mit drei Fakultäten. Wir verdeutlichen dies an zwei Beispielen in Abbildung 4:
Abbildung 4: Zwei Beispiele für Binomialkoeffizienten.
Der Binomialkoeffizient „49 über 6” entspricht damit beispielsweise der Anzahl der möglichen Ziehungen beim Lotto – nicht zu verwechseln mit der Treffer-Wahrscheinlichkeit „6 Richtige” beim Lotto, die durch eine hypergeometrische Verteilung ermittelbar ist.
Erstellen Sie eine Klasse BinomialCoefficient mit einer Methode calculate zur
Berechnung des Binomialkoeffizienten. Die folgenden Code-Fragmente sollten mit Hilfe
Ihrer Klassenimplementierung ausführbar sein:
BinomialCoefficient coeff;
for (size_t i{ 1 }; i != 10; ++i)
{
coeff.setUpper(2 * i);
coeff.setLower(i);
coeff.calculate();
std::cout
<< "Binomial "
<< coeff
<< " = "
<< coeff.value() << std::endl;
}
Ausgabe:
Binomial (2, 1) = 2
Binomial (4, 2) = 6
Binomial (6, 3) = 20
Binomial (8, 4) = 70
Binomial (10, 5) = 252
Binomial (12, 6) = 924
Binomial (14, 7) = 3432
Binomial (16, 8) = 12870
Binomial (18, 9) = 48620
Berechnen Sie der Reihe nach die Binomialkoeffizienten „2 über 1”, „4 über 2”, „8 über 4”, usw. Ab welchem Koeffizienten machen Sie auch hier die Beobachtung, dass die sehr schnell wachsenden Werte zu falschen Resultaten führen.
Methode reduce
Um dieses Problem zu lösen, kommen wir wieder auf den Trick mit der Partialbruchzerlegung zurück.
Um den Koeffizienten „n über k” auszurechnen, berechnen wir die drei Werte n!, k! und (n – k)! als PrimeDictionary-Objekte
und vereinfachen diese anschließend.
Dazu werden wir eine Methode reduce einführen, die zwei PrimeDictionary-Objekte als
Parameter hat und die Vereinfachung des ersten PrimeDictionary-Objekts um das zweite
PrimeDictionary-Objekt durchführt. Dazu betrachten wir am besten ein Beispiel in Abbildung 5:
Abbildung 5: Vereinfachung zweier PrimeDictionary-Objekte.
Ergänzen Sie nun Klasse PrimeDictionary um eine Methode reduce:
void reduce (const PrimeDictionary&);
Die Reduktion eines PrimeDictionary-Objekts durch ein zweites erfolgt dadurch, indem
man das zweite PrimeDictionary-Objekt Eintrag für Eintrag traversiert und die Potenzen
der Primzahlen von denen des ersten PrimeDictionary-Objekts subtrahiert. Verwenden Sie
zum Testen Ihrer Implementierung das Beispiel aus Abbildung 5.
Darstellung von Binomialkoeffizienten in Partialbruchdarstellung
Mit Hilfe der reduce-Methode können wir nun sehr schnell der Klasse
BinomialCoefficient eine Methode calculateLegendre hinzufügen:
PrimeDictionary calculateLegendre () const;
Zur Berechnung eines Binomialkoeffizienten zu n und k sind gemäß Abbildung 3 die drei
Fakultäten n!, k! und (n – k)! zu berechnen. Wenn Sie zuerst das PrimeDictionary-Objekt
zu n! um das PrimeDictionary-Objekt bzgl. k! reduzieren und das resultierende
PrimeDictionary-Objekt noch einmal um das PrimeDictionary-Objekt bzgl. (n – k)!
reduzieren, erhalten Sie den Binomialkoeffizienten – auch für sehr große Werte – in Partialbruchdarstellung.
Überprüfen Sie Ihre Implementierung an folgendem Codefragment:
BinomialCoefficient bin;
for (size_t i{ 1 }; i != 25; i++)
{
bin.setUpper(2 * i);
bin.setLower(i);
PrimeDictionary result = bin.calculateLegendre();
std::cout
<< "Binomial ("
<< std::setw(2) << bin.getUpper()
<< ", "
<< std::setw(2) << bin.getLower()
<< ") = "
<< result << std::endl;
}
Ausgabe:
Binomial ( 2, 1) = (2,1)
Binomial ( 4, 2) = (2,1)(3,1)
Binomial ( 6, 3) = (2,2)(3,0)(5,1)
Binomial ( 8, 4) = (2,1)(3,0)(5,1)(7,1)
Binomial (10, 5) = (2,2)(3,2)(5,0)(7,1)
Binomial (12, 6) = (2,2)(11,1)(3,1)(5,0)(7,1)
Binomial (14, 7) = (2,3)(11,1)(3,1)(13,1)(5,0)(7,0)
Binomial (16, 8) = (2,1)(11,1)(3,2)(13,1)(5,1)(7,0)
Binomial (18, 9) = (2,2)(11,1)(3,0)(13,1)(5,1)(7,0)(17,1)
Binomial (20, 10) = (2,2)(19,1)(11,1)(3,0)(13,1)(5,0)(7,0)(17,1)
Binomial (22, 11) = (2,3)(19,1)(11,0)(3,1)(13,1)(5,0)(7,1)(17,1)
Binomial (24, 12) = (2,2)(19,1)(11,0)(3,0)(13,1)(5,0)(7,1)(17,1)(23,1)
Binomial (26, 13) = (2,3)(19,1)(11,0)(3,0)(13,0)(5,2)(7,1)(17,1)(23,1)
Binomial (28, 14) = (2,3)(19,1)(11,0)(3,3)(13,0)(5,2)(7,0)(17,1)(23,1)
Binomial (30, 15) = (2,4)(19,1)(11,0)(3,2)(13,0)(5,1)(7,0)(17,1)(23,1)(29,1)
Binomial (32, 16) = (2,1)(19,1)(11,0)(3,2)(13,0)(5,1)(7,0)(17,1)(23,1)(29,1)(31,1)
Binomial (34, 17) = (2,2)(19,1)(11,1)(3,3)(13,0)(5,1)(7,0)(17,0)(23,1)(29,1)(31,1)
Binomial (36, 18) = (2,2)(19,1)(11,1)(3,1)(13,0)(5,2)(7,1)(17,0)(23,1)(29,1)(31,1)
Binomial (38, 19) = (2,3)(19,0)(11,1)(3,1)(13,0)(5,2)(7,1)(17,0)(23,1)(29,1)(31,1)(37,1)
Binomial (40, 20) = (2,2)(19,0)(11,1)(3,2)(13,1)(5,1)(7,1)(17,0)(23,1)(29,1)(31,1)(37,1)
Binomial (42, 21) = (2,3)(19,0)(11,1)(3,1)(13,1)(5,1)(7,0)(17,0)(23,1)(29,1)(31,1)(37,1)(41,1)
Binomial (44, 22) = (2,3)(19,0)(11,0)(3,1)(13,1)(5,1)(7,0)(17,0)(23,1)(29,1)(31,1)(37,1)(41,1)(43,1)
Binomial (46, 23) = (2,4)(19,0)(11,0)(3,3)(13,1)(5,2)(7,0)(17,0)(23,0)(29,1)(31,1)(37,1)(41,1)(43,1)
Binomial (48, 24) = (2,2)(19,0)(11,0)(3,2)(13,1)(5,2)(7,0)(17,0)(23,0)(29,1)(31,1)(37,1)(41,1)(43,1)(47,1)
Lösung
Quellcode: Siehe auch Github.
Auf Grund der recht umfangreichen Spezifikation aller beteiligten Klassen
können wir gleich die Implementierung betrachten, die Klasse PrimeDictionary macht den Anfang (Listing 1 und Listing 2):
01: class PrimeDictionary
02: {
03: private:
04: std::unordered_map<size_t, size_t> m_map;
05:
06: public:
07: // getter
08: size_t get(size_t key) const;
09: void set(size_t key, size_t value);
10:
11: // public interface
12: void reduce (const PrimeDictionary&);
13:
14: // output
15: friend std::ostream& operator<< (std::ostream&, const PrimeDictionary&);
16: };
Listing 1: Klasse PrimeDictionary: Definition.
01: size_t PrimeDictionary::get(size_t key) const
02: {
03: return m_map.at(key);
04: }
05:
06: void PrimeDictionary::set(size_t key, size_t value)
07: {
08: m_map[key] = value;
09: }
10:
11: void PrimeDictionary::reduce (const PrimeDictionary& dict)
12: {
13: for (const auto& [key, value] : dict.m_map) {
14:
15: size_t newCoeff = get(key) - value;
16: set(key, newCoeff);
17: }
18: }
19:
20: std::ostream& operator<< (std::ostream& os, const PrimeDictionary& dict)
21: {
22: // iterate and print keys and values using structured binding
23: for (int k = 0; const auto & [key, value] : dict.m_map) {
24: os << '(' << key << ',' << value << ')';
25: ++k;
26: if (k % 16 == 0)
27: os << '\n';
28: }
29:
30: return os;
31: }
Listing 2: Klasse PrimeDictionary: Implementierung.
Es folgt Klasse Factorial in Listing 3 und Listing 4:
01: class Factorial
02: {
03: private:
04: size_t m_n;
05: size_t m_value;
06:
07: public:
08: // c'tors
09: Factorial();
10: Factorial(size_t n);
11:
12: // getter / setter
13: size_t get() const;
14: void set(size_t);
15: size_t value() const;
16:
17: // public interface
18: void factorialRecursive();
19: void factorialIterative();
20: PrimeDictionary factorialLegendre();
21:
22: private:
23: // private helper
24: static size_t factorialRecursive(size_t n);
25: static bool isPrime(size_t);
26: };
Listing 3: Klasse Factorial: Definition.
01: size_t Factorial::get() const
02: {
03: return m_n;
04: }
05:
06: void Factorial::set(size_t n)
07: {
08: m_n = n;
09: }
10:
11: size_t Factorial::value() const
12: {
13: return m_value;
14: }
15:
16: void Factorial::factorialIterative()
17: {
18: m_value = 1;
19:
20: if (m_n <= 1) {
21: return;
22: }
23: else {
24: for (int i{ 2 }; i <= m_n; ++i)
25: m_value *= i;
26: }
27: }
28:
29: void Factorial::factorialRecursive()
30: {
31: m_value = factorialRecursive(m_n);
32: }
33:
34: PrimeDictionary Factorial::factorialLegendre()
35: {
36: // algorithm of Legendre
37: PrimeDictionary result{};
38: size_t prime{ 2 };
39: while (prime <= m_n) {
40:
41: if (size_t quo, exp; isPrime(prime)) {
42: quo = m_n / prime;
43: exp = 0;
44:
45: while (quo != 0) {
46: exp += quo;
47: quo /= prime;
48: }
49:
50: result.set(prime, exp);
51: }
52:
53: prime++;
54: }
55:
56: return result;
57: }
58:
59: size_t Factorial::factorialRecursive(size_t n)
60: {
61: return (n <= 1) ? 1 : n * factorialRecursive(n - 1);
62: }
63:
64: bool Factorial::isPrime(size_t number)
65: {
66: // the smallest prime number is 2
67: if (number <= 2) {
68: return number == 2;
69: }
70:
71: if (number % 2 == 0) {
72: return false;
73: }
74:
75: // check odd divisors from 3 to the square root of the number
76: size_t end{ static_cast<size_t>(std::ceil(std::sqrt(number))) };
77: for (size_t i{ 3 }; i <= end; i += 2) {
78: if (number % i == 0) {
79: return false;
80: }
81: }
82:
83: return true;
84: }
Listing 4: Klasse Factorial: Implementierung.
Es fehlt noch eine Klasse für Binomialkoeffizienten (Listing 5 und Listing 6):
01: class BinomialCoefficient
02: {
03: private:
04: size_t m_n;
05: size_t m_k;
06: size_t m_value;
07:
08: public:
09: // c'tors
10: BinomialCoefficient ();
11: BinomialCoefficient (size_t, size_t);
12:
13: // getter / setter
14: size_t getUpper() const;
15: size_t getLower() const;
16: void setUpper(size_t n);
17: void setLower(size_t n);
18: size_t value() const;
19:
20: // public interface
21: void calculate ();
22: PrimeDictionary calculateLegendre () const;
23: };
24:
25: // output
26: std::ostream& operator<< (std::ostream&, const BinomialCoefficient&);
Listing 5: Klasse BinomialCoefficient: Definition.
01: BinomialCoefficient::BinomialCoefficient()
02: : m_n{ 1 }, m_k{ 1 }, m_value{ 1 } {}
03:
04: BinomialCoefficient::BinomialCoefficient (size_t n, size_t k)
05: : m_n{ n }, m_k{ k }, m_value{ 0 } {}
06:
07: size_t BinomialCoefficient::getUpper() const
08: {
09: return m_n;
10: }
11:
12: size_t BinomialCoefficient::getLower() const
13: {
14: return m_k;
15: }
16:
17: void BinomialCoefficient::setUpper(size_t n)
18: {
19: m_n = n;
20: }
21:
22: void BinomialCoefficient::setLower(size_t k)
23: {
24: m_k = k;
25: }
26:
27: size_t BinomialCoefficient::value() const
28: {
29: return m_value;
30: }
31:
32: void BinomialCoefficient::calculate ()
33: {
34: if (m_k == 0 || m_k == m_n) {
35: m_value = 1;
36: }
37: else {
38: size_t a{ 1 }, b{ 1 };
39: for (size_t i{ m_n - m_k + 1 }; i <= m_n; ++i) {
40: a *= i;
41: }
42: for (int j{ 1 }; j <= m_k; ++j) {
43: b *= j;
44: }
45: m_value = a / b;
46: }
47: }
48:
49: PrimeDictionary BinomialCoefficient::calculateLegendre () const
50: {
51: Factorial facUpper{ m_n };
52: PrimeDictionary dictUpper{ facUpper.factorialLegendre() };
53:
54: Factorial facLower{ m_k };
55: PrimeDictionary dictLower{ facLower.factorialLegendre() };
56:
57: dictUpper.reduce(dictLower);
58:
59: Factorial facUpperMinusLower{ m_n - m_k };
60: PrimeDictionary dictUpperMinusLower{ facUpperMinusLower.factorialLegendre() };
61:
62: dictUpper.reduce(dictUpperMinusLower);
63:
64: return dictUpper;
65: }
66:
67: std::ostream& operator<< (std::ostream& os, const BinomialCoefficient& coeff)
68: {
69: os
70: << "("
71: << coeff.getUpper()
72: << ", "
73: << coeff.getLower()
74: << ")";
75:
76: return os;
77: }
Listing 6: Klasse BinomialCoefficient: Implementierung.
Eine Frage wollen wir im Lösungsabschnitt noch betrachten. Erinnern Sie sich: „Auf wie viele Nullen endet die Zahl 2022! ?” Mit folgendem Code-Snippet ist die Frage gelöst:
Factorial f(2022);
PrimeDictionary primes = f.factorialLegendre();
size_t numFactorsOf5 = primes.get(5);
std::cout << "Factors of 5: " << numFactorsOf5 << "." << std::endl;
Ausgabe:
Factors of 5: 503.
There‘s more
Die drei Klassen PrimeDictionary, Factorial und BinomialCoefficient sind bzgl. ihrer
Instanzvariablen mit dem Datentyp size_t realisiert. Diese harte Festlegung könnte man mit Klassentemplates vermeiden.
Es bietet sich an, diese Klassen als Templates zu realisieren.
Literatur
Einige Beispiele und Anregungen zu dem Satz von Legende stammen aus dem Aufsatz „Die Sätze von Legendre und Tchebychef” (abgerufen am 27. März 2022).