In dieser Fallstudie betrachten wir ein sehr „martialisches” Problem, das durch den jüdischen Historiker Flavius Josephus überliefert worden ist. Dieser soll im römisch–jüdischen Krieg mit 41 Kameraden den Selbstmord der Gefangenschaft vorgezogen haben. Details finden Sie gleich weiter unten vor – umso interessanter die Fragestellung, wie Informatiker bei dieser Fallstudie ins Spiel kommen: Josephus fand nämlich heraus, an welche Position im Kreis er sich stellen musste, um als letzter übrig zu bleiben, also um überleben zu können.
Damit sind schlagartig vielen Türen der Informatik geöffnet, zum Beispiel einfach-verkettete Listen, Arrays und sogar das Prinzip der Vererbung, um nur einige wenige anzusprechen. Lassen Sie sich überraschen, wie wir mit den Hilfsmitteln des Modern C++ die Lösung des Josephus-Problems bestimmen.
Lernziele
- Default-Initialisierung für Member-Variablen
- Delegation von Konstruktoren (nun auch in C++ enthalten)
- Bereichs-basierte
for-Wiederholungsschleife (Range-Based For Loop) mit Variablendeklaration - Container
std::forward_list<T> - Neue Schlüsselwörter
overrideundfinalergänzend zuvirtual - STL-Algorithmus
std::find_if
Aufgabe
Das Meisterwerk des Historikers Flavius Josephus ist seine geschichtliche Darstellung des Jüdischen Krieges. Einer Legende zufolge war er während dieses Krieges Mitglied einer 41-köpfigen jüdischen Rebellenbande, die im Jahre 67 n. Chr. in der galiläischen Stadt Jotopata ein Zentrum des antirömischen Widerstandes bildete. Nach 47-tägiger Belagerung gelang es den Römern unter der Führung ihres Kaisers Vespasian jedoch, die Stadt einzunehmen. Die Rebellen beschlossen, den Freitod einer Gefangenschaft vorzuziehen. Vergebens beschwor Josephus seine Mitstreiter, davon abzulassen. Um wenigstens sich zusammen mit einem unbekannten Mitverschwörer vor dieser Freitod-Orgie zu retten, schlug er als Tötungsritual den alten römischen Brauch der Decimatio (Dezimierung) vor: Zuerst mussten sich die Rebellen in einem Kreis herum aufzustellen, danach sollte sich jeder dritte nacheinander im Kreis das Leben nehmen. Josephus jedoch konnte dank seiner mathematischen Begabung schnell ausrechnen, wo er und sein Freund im Kreis stehen mussten, um als Letzte übrig zu bleiben und somit dem Tode zu entkommen.
Anforderungen an das Programm
Schreiben Sie ein Programm, dass berechnet, an welche Stelle des Kreises Josephus sich und seinen Freund stellte, um zu überleben? Zum Entwurf einer Lösung können sehr unterschiedliche Datenstrukturen zum Einsatz kommen. Investieren Sie zunächst genügend Zeit in die Ausgestaltung eines Entwurfs, bevor Sie mit der Implementierung anfangen.
Bei 17 Soldaten sollte die Ausgabe des Programms wie folgt aussehen, wenn jeder dritte Soldat ausgesondert wird:
Number of soldiers: 17
Eliminating: Each 3. soldier
Removed 3 [1,2,4,5,6,7,8,9,10,11,12,13,14,15,16,17]
Removed 6 [1,2,4,5,7,8,9,10,11,12,13,14,15,16,17]
Removed 9 [1,2,4,5,7,8,10,11,12,13,14,15,16,17]
Removed 12 [1,2,4,5,7,8,10,11,13,14,15,16,17]
Removed 15 [1,2,4,5,7,8,10,11,13,14,16,17]
Removed 1 [2,4,5,7,8,10,11,13,14,16,17]
Removed 5 [2,4,7,8,10,11,13,14,16,17]
Removed 10 [2,4,7,8,11,13,14,16,17]
Removed 14 [2,4,7,8,11,13,16,17]
Removed 2 [4,7,8,11,13,16,17]
Removed 8 [4,7,11,13,16,17]
Removed 16 [4,7,11,13,17]
Removed 7 [4,11,13,17]
Removed 17 [4,11,13]
Removed 13 [4,11]
Removed 4 [11]
Last eliminated soldier: 4
Last alive soldier: 11
Die Ausgabe kann durch das nachfolgende Codefragment erzeugt werden. Sie dürfen hiervon abweichen und eigene Vorstellungen umsetzen:
Josephus j{ 17 };
j.setPassBy(3);
std::cout << "Number of soldiers: " << j.count() << std::endl;
std::cout << "Eliminating: Each " << j.passBy() << ". soldier" << std::endl << std::endl;
while (j.alive() > 1)
{
j.eliminateNextSoldier();
std::cout << "Removed ";
std::cout.width(2);
std::cout << j.lastEliminated() << " " << j << std::endl;
}
std::cout << std::endl;
std::cout << "Last eliminated soldier: " << j.lastEliminated() << std::endl;
std::cout << "Last alive soldier: " << j.lastAlive() << std::endl;
Wie lautet nun die Antwort des Josephus-Problems in seiner historisch überlieferten Version? Es handelt sich dabei – einschließlich Josephus – um 41 Soldaten und es wird jeweils jeder dritte Soldat getötet.
Lösung
Quellcode: Siehe auch Github.
Zur Lösung des Problems bieten sich bzgl. des Einsatzes von Datenstrukturen prinzipiell zwei Möglichkeiten an:
Entweder der Aufbau einer einfach verketteten Liste, in der jeder Knoten einen Soldaten der Rebellenbande darstellt.
Oder aber ein Array vom Typ bool, das pro Rebell einen Eintrag besitzt.
Für beide Varianten stellen wir eine Lösung vor.
Zur Vertiefung bzw. Wiederholung elementarer programmiersprachlicher C++–Konstrukte im Umfeld der Vererbung
stellen wir auf Basis des objekt-orientierten Entwurfs zunächst eine Schnittstelle IJosephus vor (Listing 1).
Schnittstellen lassen sich in C++ mit so genannten „pure-virtuellen” Methoden nachahmen,
in anderen Programmiersprachen gibt es eigens dafür ein programmiersprachliches Konstrukt mit dem Schlüsselwort interface.
01: class IJosephus
02: {
03: public:
04: // getter/setter
05: virtual size_t count() const = 0;
06: virtual size_t alive() const = 0;
07: virtual size_t lastEliminated() const = 0;
08: virtual size_t lastAlive() const = 0;
09: virtual size_t passBy() const = 0;
10: virtual void setPassBy(int passby) = 0;
11:
12: // public interface
13: virtual bool eliminateNextSoldier() = 0;
14: virtual void eliminateAll() = 0;
15: };
Listing 1: Klasse IJosephus: Definition.
Zur IJosephus-Schnittstelle bieten wir eine unvollständige Realisierung in Gestalt einer Klasse Josephus an,
die nachfolgend ihrerseits als Basis zweier konkreter Klassen JosephusArrayImpl und JosephusForwardListImpl fungiert.
In Listing 2 und Listing 3 stellen wie die abstrakte Basisklasse Josephus vor.
Die zahlreichen Eigenschaften (getter/setter-Methoden) der IJosephus-Schnittstelle lassen sich hier zentral zusammenfassen:
01: class Josephus : public IJosephus
02: {
03: protected:
04: size_t m_count; // total number of soldiers
05: size_t m_alive; // number of alive soldiers
06: size_t m_lastEliminated{ 0 }; // last eliminated soldier
07: size_t m_lastAlive{ 0 }; // number of surviving soldier
08: size_t m_passby{ DefaultPassBy }; // "decimatio"
09:
10: public:
11: // c'tors
12: Josephus();
13: Josephus(size_t count, size_t passby);
14:
15: // public interface
16: virtual void eliminateAll() override final;
17:
18: // getter/setter
19: virtual size_t count() const override { return m_count; }
20: virtual size_t alive() const override { return m_alive; }
21: virtual size_t lastEliminated() const override { return m_lastEliminated; }
22: virtual size_t lastAlive() const override { return m_lastAlive; }
23: virtual size_t passBy() const override { return m_passby; }
24: virtual void setPassBy(int passby) override { m_passby = passby; }
25: };
Listing 2: Klasse Josephus: Definition.
01: // c'tors
02: Josephus::Josephus() : Josephus{ NumSoldiers, DefaultPassBy } {}
03:
04: Josephus::Josephus(size_t count, size_t passby)
05: : m_count{ count }, m_alive{ count }, m_passby{ passby } {}
06:
07: void Josephus::eliminateAll()
08: {
09: while (eliminateNextSoldier())
10: ;
11: }
Listing 3: Klasse Josephus: Implementierung.
Nun sind wir bei der noch ausstehenden Realisierung der eigentlichen Funktionalität des Josephus-Problems angekommen.
Zwei einfache Ansätze lassen sich auf Basis eines eindimensionalen Felds (vom Typ bool)
oder einer einfach-verketteten Liste verfolgen. Natürlich wollen wir soweit möglich auf den Werkzeugkasten der STL zurückgreifen,
es bieten sich die beiden Klassen std::array<T> bzw. std::forward_list<T> an.
Lösung mit std::array<T> als zentraler Datenstruktur
In einem Array vom Typ bool können Sie mit den beiden Werten true und false hinterlegen,
ob der i.-te Soldat während des Auszählens noch am Leben ist oder nicht.
Das Auszählen selbst erfolgt durch geschicktes Traversieren des Arrays, wobei Sie im Wesentlichen nur darauf achten müssen,
keine Zugriffsverletzung mit einem unzulässigen Index zu erzeugen.
Zur Illustration finden Sie in Abbildung 1 ein Beispiel mit 12 Soldaten und Auszählabstand 3 vor.
Am Ende bleiben in dem Feld zwei Einträge mit einem true-Wert übrig, es handelt sich um die Soldaten 3 und 8.
Abbildung 1: Beispiel des Josephus-Problems mit Datenstruktur Array.
Beginnen wir in Listing 4
mit Betrachtung einer Klasse JosephusArrayImpl, die die Klasse Josephus spezialisiert und dazu ein eindimensionales Feld
des Typs std::array<bool> verwendet. Der einzige Wehrmutstropfen bei diesem Lösungsansatz besteht darin, dass std::array<T>-Instanzen ihre Länge
zur Übersetzungszeit kennen müssen. Wir definieren dazu an zentraler Stelle im Programm eine Variable NumSoldiers:
constexpr size_t NumSoldiers = 17; // number of soldiers
In Listing 4 (Schnittstelle) und Listing 5 (Implementierung) finden Sie die Details zur Klasse JosephusArrayImpl vor:
01: class JosephusArrayImpl : public Josephus
02: {
03: private:
04: // array of boolean states: alive or not
05: std::array<bool, NumSoldiers> m_soldiers{ };
06: size_t m_current; // current index into array
07:
08: public:
09: // c'tors
10: JosephusArrayImpl();
11: JosephusArrayImpl(size_t count, size_t passby);
12:
13: // public interface
14: virtual bool eliminateNextSoldier() override;
15:
16: private:
17: // private helper methods
18: void init();
19: void moveToNextAliveSoldier();
20: void nextIndex();
21:
22: // output
23: friend std::ostream& operator<< (std::ostream&, JosephusArrayImpl&);
24: };
Listing 4: Klasse JosephusArrayImpl: Schnittstelle.
01: // c'tors
02: JosephusArrayImpl::JosephusArrayImpl() : JosephusArrayImpl{ NumSoldiers, DefaultPassBy } {}
03:
04: JosephusArrayImpl::JosephusArrayImpl(size_t count, size_t passby) : Josephus{ count, passby } {
05: init();
06: }
07:
08: // public interface
09: bool JosephusArrayImpl::eliminateNextSoldier()
10: {
11: // more than one soldier alive?
12: if (m_alive == 1) {
13: return false;
14: }
15:
16: for (int i = 0; i < m_passby - 1; i++) {
17: moveToNextAliveSoldier();
18: nextIndex(); // skip found alive soldier
19: }
20:
21: moveToNextAliveSoldier();
22:
23: // kill 'n'.th soldier
24: m_soldiers[m_current] = false;
25: m_alive--;
26: m_lastEliminated = m_current + 1;
27:
28: // compute index of last alive soldier
29: if (m_alive == 1) {
30:
31: std::array<bool, NumSoldiers>::iterator it = std::find_if(
32: std::begin(m_soldiers),
33: std::end(m_soldiers),
34: [](bool b) {
35: return b == true;
36: }
37: );
38:
39: m_lastAlive = it - std::begin(m_soldiers) + 1;
40: }
41:
42: return true;
43: }
44:
45: // private helper methods
46: void JosephusArrayImpl::init()
47: {
48: for (bool& entry : m_soldiers) {
49: entry = true;
50: }
51:
52: m_current = 0;
53: }
54:
55: void JosephusArrayImpl::moveToNextAliveSoldier()
56: {
57: while (m_soldiers[m_current] == false) {
58: nextIndex(); // move index to next entry
59: }
60: }
61:
62: void JosephusArrayImpl::nextIndex()
63: {
64: // move index to next entry
65: m_current++;
66: if (m_current >= m_count) {
67: m_current = 0;
68: }
69: }
70:
71: // output
72: std::ostream& operator<< (std::ostream& os, JosephusArrayImpl& j)
73: {
74: os << '[';
75: size_t save = j.m_current; // save current state of position index
76: j.m_current = 0;
77:
78: int count = 0;
79: do {
80: j.moveToNextAliveSoldier();
81: os << (j.m_current + 1);
82:
83: count++;
84: if (count < j.alive())
85: os << ',';
86:
87: j.nextIndex();
88: }
89: while (count < j.alive());
90:
91: os << ']';
92: j.m_current = save; // restore current state of position index
93: return os;
94: }
Listing 5: Klasse JosephusArrayImpl: Implementierung.
Lösung mit std::forward_list<T> als zentraler Datenstruktur
Ordnen Sie n nummerierte Soldaten in einer einfach verketteten Liste an. Wenn Sie den Knoten des letzten Soldaten auf den Knoten des ersten Soldaten zeigen lassen, kommen Sie der Realität sehr nahe! Dann wird, beginnend mit dem ersten Soldaten, jeder m.-te Soldat (Knoten) aus der Liste entfernt, wobei der Kreis geschlossen bleibt. Auf diese Weise erkennt man, welche zwei Soldaten als letztes überleben!
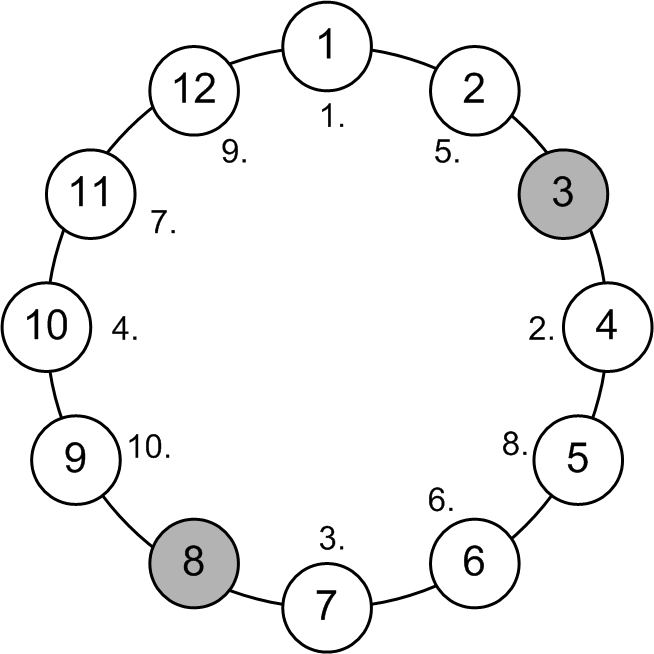
Abbildung 2: Beispiel des Josephus-Problems mit Datenstruktur „verkettete Liste”.
Am Beispiel aus Abbildung 2 können Sie die Arbeitsweise des „Auszählens” nachverfolgen. 12 Soldaten sind hier in einem Kreis angeordnet. Nacheinander bringt sich jeder dritte um. Soldat 1 stirbt zuerst, danach Soldat 4 usw. Neben den Soldaten steht die jeweilige Nummer in der Eliminationsreihenfolge. Am Schluss bleiben die Soldaten 3 und 8 übrig.
Für die Template Klasse std::forward_list<T> benötigen wir ein Template Argument.
Zu diesem Zweck definieren wir die Hilfsklasse Soldier (Listing 6), die in der verketteten Liste ein einzelnes Listenelement darstellt:
01: class Soldier
02: {
03: private:
04: size_t m_number{ 1 };
05:
06: public:
07: // c'tors
08: Soldier() = delete;
09: Soldier(size_t number) : m_number{ number } {};
10:
11: // getter
12: size_t getNumber() { return m_number; }
13:
14: // operators
15: size_t operator()() const { return m_number; };
16: };
Listing 6: Klasse Soldier.
Auf Basis der Klasse Soldier in Listing 6 und einer verketteten Liste lässt sich der letzte überlebende Soldat nun
mit Hilfe einer Klasse JosephusForwardListImpl wie in Listing 7 und Listing 8 gezeigt ermitteln.
Wir verzichten allerdings darauf, das letzte Element in der Liste auf das Erste wiederum zeigen zu lassen.
Die Methode eliminateNextSoldier zollt diesem Umstand Beachtung, in dem sie
bei Erreichen des Listenendes wieder zurück zum Anfang schaltet.
Studieren Sie zu diesem Zweck genau den Einsatz der Methoden
begin(), end(), before_begin(), erase_after() und push_front()
in Listing 8.
01: class JosephusForwardListImpl : public Josephus
02: {
03: private:
04: // linked list of Soldier objects
05: std::forward_list<Soldier> m_soldiers;
06: std::forward_list<Soldier>::iterator m_current;
07:
08: public:
09: // c'tors
10: JosephusForwardListImpl();
11: JosephusForwardListImpl(size_t count, size_t passby);
12:
13: // public interface
14: virtual bool eliminateNextSoldier() override;
15:
16: private:
17: // private helper methods
18: void init();
19:
20: // output
21: friend std::ostream& operator<< (std::ostream&, const JosephusForwardListImpl&);
22: };
Listing 7: Klasse JosephusForwardListImpl: Schnittstelle.
01: // c'tors
02: JosephusForwardListImpl::JosephusForwardListImpl()
03: : JosephusForwardListImpl{ NumSoldiers, DefaultPassBy } {}
04:
05: JosephusForwardListImpl::JosephusForwardListImpl(size_t count, size_t passby)
06: : Josephus{ count, passby } {
07: init();
08: }
09:
10: // public interface
11: bool JosephusForwardListImpl::eliminateNextSoldier()
12: {
13: // more than one soldier alive?
14: if (m_alive == 1) {
15: return false;
16: }
17:
18: // locate next soldier
19: std::forward_list<Soldier>::iterator preceding;
20:
21: for (size_t i = 0; i != m_passby - 1; ++i) {
22:
23: preceding = m_current;
24: ++m_current;
25:
26: if (m_current == m_soldiers.end()) {
27: preceding = m_soldiers.before_begin();
28: m_current = m_soldiers.begin();
29: }
30: }
31:
32: m_lastEliminated = (*m_current).getNumber();
33:
34: ++m_current;
35: if (m_current == m_soldiers.end()) {
36: m_current = m_soldiers.begin();
37: }
38:
39: // remove soldier from list
40: m_soldiers.erase_after(preceding);
41: m_alive--;
42:
43: // compute index of last alive soldier
44: if (m_alive == 1) {
45: m_lastAlive = (*m_current).getNumber();
46: }
47:
48: return true;
49: }
50:
51: // private helper methods
52: void JosephusForwardListImpl::init()
53: {
54: for (size_t i = 0; i != m_count; ++i) {
55: m_soldiers.push_front(Soldier{ m_count - i });
56: }
57:
58: m_current = m_soldiers.begin();
59: }
60:
61: // output
62: std::ostream& operator<< (std::ostream& os, const JosephusForwardListImpl& josephus)
63: {
64: os << '[';
65: for (size_t i = 1; const Soldier & soldier : josephus.m_soldiers) {
66: os << soldier();
67: if (i < josephus.m_alive) {
68: os << ',';
69: ++i;
70: }
71: }
72: os << ']';
73: return os;
74: }
Listing 8: Klasse JosephusForwardListImpl: Implementierung.
Mit folgendem Testrahmen kommen wir nun dem Rätsel auf die Spur, an welche Stelle im Kreis sich Josephus gestellt hat:
std::shared_ptr<IJosephus> sp = std::make_shared<JosephusForwardListImpl>(41, 3);
sp->setPassBy(3);
std::cout << "Number of soldiers: " << sp->count() << std::endl;
std::cout << "Eliminating: Each " << sp->passBy() << ". soldier" << std::endl << std::endl;
while (sp->alive() > 1)
{
sp->eliminateNextSoldier();
std::cout << "Removed " << std::setw(2) << sp->lastEliminated() << std::endl;
}
std::cout << std::endl;
std::cout << "Last eliminated soldier: " << sp->lastEliminated() << std::endl;
std::cout << "Last alive soldier: " << sp->lastAlive() << std::endl;
Ausgabe des Programms:
Number of soldiers: 41
Eliminating: Each 3. soldier
Removed 3
Removed 6
Removed 9
Removed 12
Removed 15
Removed 18
Removed 21
Removed 24
Removed 27
Removed 30
Removed 33
Removed 36
Removed 39
Removed 1
Removed 5
Removed 10
Removed 14
Removed 19
Removed 23
Removed 28
Removed 32
Removed 37
Removed 41
Removed 7
Removed 13
Removed 20
Removed 26
Removed 34
Removed 40
Removed 8
Removed 17
Removed 29
Removed 38
Removed 11
Removed 25
Removed 2
Removed 22
Removed 4
Removed 35
Removed 16
Last eliminated soldier: 16
Last alive soldier: 31
Der Legende nach stellte Josephus sich an die 16. Stelle und blieb damit als Vorletzter übrig. Er konnte auf diese Weise den letzten, schwächeren Mann an der 31. Position überwältigen. Beide ergaben sich den Römern und konnten auf diese Weise ihr Leben retten.