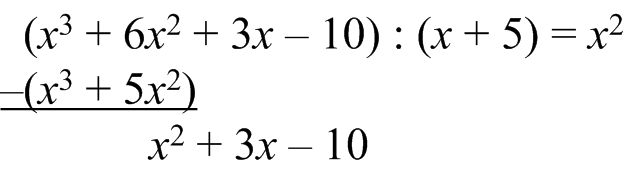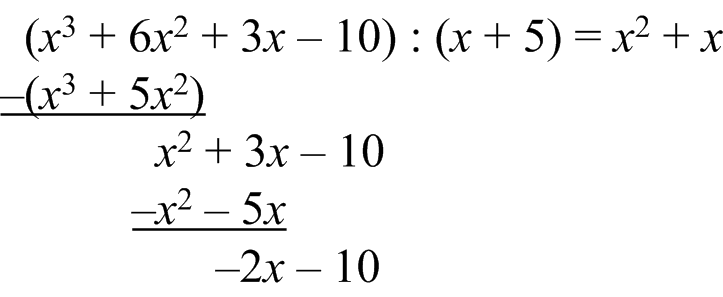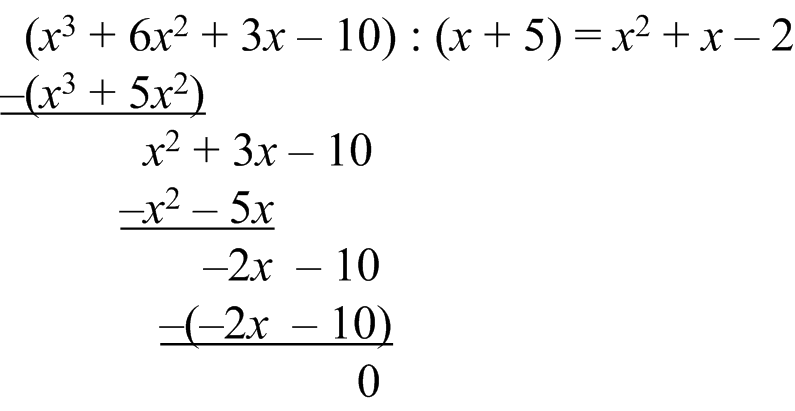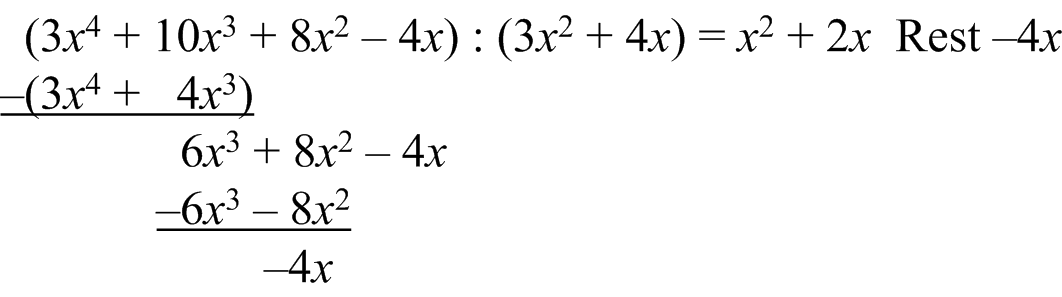Gegenstand dieser Aufgabe sind Polynomfunktionen, kurz auch Polynome genannt. Formal ist ein Polynom als Summe von Vielfachen von Potenzen einer Variablen x definiert:
Pn(x) = anxn + an-1xn-1 + … + a2x2 + a1x + a0.
Entwickeln Sie eine Klasse Polynom, die – möglichst einfallsreich – die unterschiedlichen Konstrukte
(Instanzvariablen, Konstruktoren, Methoden, inklusive getter- und setter-Methoden, Lambda-Funktionen, Operatoren usw.)
zur Definition einer Klasse in „Modern C++” in Anspruch nimmt.
Lernziele
- Einheitliche Initialisierung
- Initialisierungsliste (
std::initializer_list<T>) - STL-Klasse
std::vector<T> - C++ Iteratorenkonzept
- Container-Methoden
rbegin()undrend() std::moveaus dem Standard Library Header<algorithm>- STL-Algorithmen
std::begin,std::end,std::for_each,std::next,std::transform,std::find_if
Einführung
Die Variable x wie auch die Koeffizienten ai können beliebige reelle Werte annehmen, wir sprechen von einem reellen Polynom. Als Grad des Polynoms wird der höchste Exponent n bezeichnet, für den der Koeffizient des Ausdrucks anxn nicht Null ist. Dieser Koeffizient wird auch Leitkoeffizient genannt.
Konstruktoren und getter-/setter-Methoden
Die Konstruktoren und getter-/setter-Methoden der Klasse Polynom finden Sie in Tabelle 1 genauer spezifiziert vor:
| Element | Beschreibung |
|---|---|
| Konstruktor | Polynom() = default;Der Standardkonstruktor erzeugt ein Null-Polynom. Dieses besitzt den Rang 0, der Leitkoeffizient hat ebenfalls den Wert 0: P0(x) = 0. |
| Benutzerdefinierter Konstruktor | Polynom(const std::initializer_list<double>&);Der benutzerdefinierte Konstruktor legt ein Polynom mit den Koeffizienten einer variabel lange Liste von Koeffizienten an. Das erste Element des Arrays ist dem niederwertigsten Koeffizienten zuzuordnen, das letzte dem höchstwertigen. |
getter rank() |
size_t rank() const;Liefert den Grad des Polynoms zurück. |
getter zero() |
bool zero() const;Liefert den Wert true zurück, wenn das aktuelle Polynom das Null-Polynom ist, andernfalls false. |
Tabelle 1: Konstruktoren und getter-/setter-Methoden der Klasse Polynom.
Es folgen einige Beispiele:
Polynom p1{ };
Polynom p2{ -5.0, +6.0, -7.0 };
std::cout << p1 << std::endl;
std::cout << p1.rank() << std::endl;
std::cout << std::boolalpha << p1.zero() << std::endl;
std::cout << p2 << std::endl;
std::cout << p2.rank() << std::endl;
std::cout << std::boolalpha << p2.zero() << std::endl;
Ausgabe:
0
0
true
-7x^2+6x^1-5
2
false
Für die Ausgabe eines Polynoms auf der Konsole implementieren Sie den Ausgabeoperator << geeignet (Tabelle 2):
| Element | Beschreibung |
|---|---|
Operator << |
friend std::ostream& operator<< (std::ostream&, const Polynom&);Gibt das Polynom p auf der Konsole aus. |
Tabelle 2: Ausgabeoperator << der Klasse Polynom.
Beispiel:
Polynom p{ 2.0, -4.0, 0.0, 3.0 };
std::cout << p << std::endl;
Ausgabe:
3x^3+0x^2-4x^1+2x^0
oder etwas eleganter
3x^3-4x^1+2
Operatoren
Polynome besitzen eine Reihe zentraler Operatoren und Methoden, um sie beispielsweise zu addieren oder zu multiplizieren oder aber um ihren Wert für ein bestimmtes Argument zu berechnen. Im Folgenden finden Sie einige Wiederholungen der Grundlagen von Polynomen vor.
Die Addition eines Polynoms des Grades n mit einem Polynom des Grades m ergibt ein Polynom des Grades max(n, m). Die Koeffizienten des Ergebnispolynoms werden jeweils durch Addition des Koeffizienten ai des einen Polynoms mit dem passenden Koeffizienten bi des anderen Polynoms gebildet. Für die beiden Polynome
P(x) = 3x3 - 4x + 2
und
Q(x) = 5x2 + 3x + 3
lautet die Summe
P(x) + Q(x) = 3x3 + 5x2 - x + 5.
Analog zur Addition von Polynomen ist ihre Subtraktion definiert, es werden einfach nur die entsprechenden Koeffizienten voneinander subtrahiert.
Die Polynommultiplikation eines Polynoms des Grades n mit einem Polynom des Grades m ergibt ein Polynom des Grades n+m. Bei der Polynommultiplikation multiplizieren Sie jedes aixi des einen Polynoms mit allen bjxj des anderen Polynoms und summieren die Koeffizienten der jeweilig passenden Grade. Das Produkt der Polynome des letzten Beispiels lautet:
P(x) * Q(x) = 15x5 + 9x4 - 11x3 - 2x2 - 6x + 6.
Im Prinzip können Sie das Multiplizieren zweier Polynome auch als Ausmultiplizieren von Klammern ansehen:
(3x3 - 4x + 2) * (5x2 + 3x + 3)
= 15x5 + 9x4 + 9x3 - 20x3 - 12x2 - 12x + 10x2 + 6x + 6
= 15x5 + 9x4 - 11x3 - 2x2 - 6x + 6.
Auf die Division gehen wir etwas ausführlicher ein. Wir teilen das Polynom x3 + 6x2 + 3x - 10 durch das Polynom x + 5. Zuerst müssen wir bestimmen, wie oft x + 5 in das erste Polynom hineinpasst. Man betrachtet dabei stets die höchste Potenz aus beiden Polynomen (also x3 aus dem ersten und x aus dem zweiten Polynom) und berechnet, wie oft x in x3 hineinpasst. Anders herum formuliert: Mit was muss man x multiplizieren, so dass x3 herauskommt? Natürlich mit x2, das erste Teilresultat der Division ergibt sich nun zu
(x3 + 6x2 + 3x - 10) : (x + 5) = x2
Wie bei der Division von ganzen Zahlen multipliziert man jetzt den neuen Bestandteil des Ergebnisses mit dem Divisor und schreibt ihn „passend” unter den Dividenden, also gleiche Potenzen von x sind jeweils untereinander zu schreiben:
(x3 + 6x2 + 3x - 10) : (x + 5) = x2
x3 + 5x2
Nun wird die Subtraktion durchgeführt und anschließend werden alle restlichen Glieder des Polynoms „heruntergeholt”:
Der Rest hat nur noch den Polynomgrad 2, wir haben also das Problem schon um einen Grad verringert. Nun stehen wir wieder vor der Ausgangsfrage: Wie oft passt das x aus dem Divisor in das x2, die höchste Potenz des Restes. Offensichtlich x-Mal, damit ist der nächste Summand des Quotienten (des Ergebnisses) +x:
Die jetzt noch zu beantwortende Frage lautet „Wie oft passt x in -2x?”. Offensichtlich -2-Mal, und die (letzte) Subtraktion sieht nun so aus:
Dass diese Polynomdivision keinen Rest besitzt, ist in der Tat Zufall – oder um es doch ehrlich zu sagen: Ich habe es mit Absicht so hingedeichselt :-). Es kann allerdings auch der Fall vorliegen, dass das Restpolynom nicht mehr durch das Divisorpolynom teilbar ist. In diesem Fall weist die Polynomdivision einen „Rest” auf. Neben der Division gibt es daher auch die Modulo-Operation für Polynome, also die Bestimmung des Restpolynoms bei Polynomdivision, siehe dazu folgendes Beispiel:
Damit kommen wir zur Auswertung des Polynoms an einer bestimmten Stelle x. Um uns unnötige Berechnungen von Potenzen zu ersparen, berechnen wir den Wert mit dem sogenannten Horner-Schema. Die Arbeitsweise des Horner-Schemas kann man leicht erkennen, wenn wir es konkret für Polynome bis zum dritten Grad einmal exemplarisch betrachten:
P0(x) = a0,
P1(x) = a1x + a0,
P2(x) = a2x2 + a1x + a0 = (a2x + a1)x + a0,
P3(x) = a3x3 + a2x2 + a1x + a0 = ((a3x + a2)x + a1)x + a0.
Jetzt wird die Wiederholstruktur des Horner-Schemas deutlich erkennbar:
y3 = a3.
y2 = a2 + x * y3.
y1 = a1 + x * y2.
y0 = a0 + x * y1.
Der gesuchte Polynomwert entspricht nun dem Wert y0. An Hand dieses recht einfachen Beispiels sollte die Arbeitsweise des Horner-Schemas erkennbar geworden sein, weitere Erläuterungen finden Sie in der einschlägigen Literatur vor.
Abschließend treffen wir eine Aussage zum Vergleich zweier Polynome: Ein Polynom ist größer als ein anderes, wenn sein Grad größer ist. Ist der Grad gleich, sind der Reihe nach alle Koeffizienten, beginnend bei an, zu vergleichen. Sind alle Koeffizienten gleich, sind die Polynome gleich.
Informationen bezüglich der einzelnen C++-Operatorensignaturen der soeben betrachteten Polynomfunktionen finden Sie nun in Tabelle 3 vor:
| Element | Beschreibung |
|---|---|
Operator + |
friend Polynom operator+ (const Polynom&, const Polynom&);Addition zweier Polynome. |
Operator - |
friend Polynom operator- (const Polynom&, const Polynom&);Subtraktion zweier Polynome. |
Operator * |
friend Polynom operator* (const Polynom&, const Polynom&);Multiplikation zweier Polynome. |
Operator / |
friend Polynom operator/ (const Polynom&, const Polynom&);Division zweier Polynome. |
Operator % |
friend Polynom operator% (const Polynom&, const Polynom&);Rest bei Division zweier Polynome. |
Tabelle 3: Arithmetische Operatoren der Klasse Polynom.
In Ergänzung zu Tabelle 3 sollten wir nicht vergessen, dass es die beiden Operatoren + und - neben ihrer binären Stelligkeit
auch unär gibt (Tabelle 4):
| Element | Beschreibung |
|---|---|
Operator + |
friend Polynom operator+ (const Polynom&);Unärer Plus – Das Ergebnis des unären Plus-Operators ( +) ist der Wert seines Operanden. |
Operator - |
friend Polynom operator- (const Polynom&);Negation eines Polynoms (Vorzeichenwechsel) – Der unäre Negations-Operator ( -) erzeugt den negativen Wert seines Operanden. |
Tabelle 4: Die beiden Operatoren + und - der Klasse Polynom in ihrer unären Ausprägung.
Zum Testen Ihrer Realisierung führen wir einige Testbeispiele auf:
Beispiel:
Polynom p1{ 2.0, -4.0, 0.0, 3.0 };
Polynom p2{ 3.0, 3.0, 5.0 };
Polynom p3 = p1 + p2;
std::cout << p1 << std::endl;
std::cout << p2 << std::endl;
std::cout << p3 << std::endl;
Ausgabe:
3x^3-4x^1+2
5x^2+3x^1+3
3x^3+5x^2-x^1+5
Beispiel:
Polynom p1{ 2.0, -4.0, 0.0, 3.0 };
Polynom p2{ 3.0, 3.0, 5.0 };
Polynom p3 = p1 - p2;
std::cout << p3 << std::endl;
Ausgabe:
3x^3-5x^2-7x^1-1
Beispiel:
Polynom p1{ 2.0, -4.0, 0.0, 3.0 };
Polynom p2{ 3.0, 3.0, 5.0 };
std::cout << "p1*p2: " << p1*p2 << std::endl;
Ausgabe:
p1*p2: 15x^5+9x^4-11x^3-2x^2-6x^1+6
Beispiel:
Polynom p1{ 4.0, -2.0, 6.0, 5.0, -1.0, 2.0 };
Polynom p2{ 4.0, 2.0, 0.0, 1.0 };
std::cout << p1 << std::endl;
std::cout << p2 << std::endl;
std::cout << "p1/p2: " << p1/p2 << std::endl;
Ausgabe:
2x^5-x^4+5x^3+6x^2-2x^1+4
x^3+2x^1+4
p1/p2: 2x^2-x^1+1
Beispiel:
Polynom p1{ 0, -4, 8, 10, 3 };
Polynom p2{ 0, 4, 3 };
std::cout << "p1%p2: " << p1 % p2 << std::endl;
Ausgabe:
p1%p2: -4x^1
Hinweis: Die Division zweier Polynome kann in der Realisierung dadurch vereinfacht werden,
wenn Sie die Klasse Polynom um eine Hilfsmethode sowie zwei Hilfsoperatoren ergänzen (Tabelle 5):
| Element | Beschreibung |
|---|---|
Operator * |
friend Polynom operator* (const Polynom& p, double scalar);friend Polynom operator* (double scalar, const Polynom& p);Multiplikation eines Polynoms p mit der Konstanten scalar. |
Methode multiplyX |
void multiplyX(size_t k);Multiplikation eines Polynoms mit x oder einer Potenz von x. Der Parameter k spezifiziert den Exponenten von x, beschreibt also den Term xk. |
Tabelle 5: Hilfsmethoden/-operatoren der Klasse Polynom.
Die arithmetischen Operatoren sollten in der Klasse Polynom auch in der Wertzuweisungsform vorhanden sein, siehe Tabelle 6:
| Element | Beschreibung |
|---|---|
Operator += |
friend Polynom& operator+= (Polynom&, const Polynom&);Additionswertzuweisung. |
Operator -= |
friend Polynom& operator-= (Polynom&, const Polynom&);Subtraktionswertzuweisung. |
Operator *= |
friend Polynom& operator*= (Polynom&, const Polynom&);Multiplikationswertzuweisung. |
Operator /= |
friend Polynom& operator/= (Polynom&, const Polynom&);Divisionswertzuweisung. |
Operator %= |
friend Polynom& operator%= (Polynom&, const Polynom&);Modulo Wertzuweisung. |
Tabelle 6: Arithmetische Operatoren der Klasse Polynom in der Wertzuweisungsform.
Auch zu den Operatoren von Tabelle 6 führen wir ein Beispiel auf:
Beispiel:
Polynom p1{ 1.0, 2.0, 3.0 };
Polynom p2{ 3.0, 2.0, 1.0 };
std::cout << p1 << std::endl;
std::cout << p2 << std::endl;
p1 += p2;
std::cout << p1 << std::endl;
p1 -= p2;
std::cout << p1 << std::endl;
p1 *= p2;
std::cout << p1 << std::endl;
p1 /= p2;
std::cout << p1 << std::endl;
p1 %= p2;
std::cout << p1 << std::endl;
Ausgabe:
3x^2+2x^1+1
x^2+2x^1+3
4x^2+4x^1+4
3x^2+2x^1+1
3x^4+8x^3+14x^2+8x^1+3
3x^2+2x^1+1
-4x^1-8
Bislang haben uns wir ausschließlich dem „Ring der Polynome” zugewendet, wie ein Mathematiker sagen würde,
also dem Verknüpfen von Polynomen mit Operatoren.
Um die mathematische Schreibweise für die Auswertung eines Polynoms p an der Stelle y nachzuahmen,
bieten sich in C++ gleich zwei Operatoren an: Der Index-Operator [] sowie der Funktionsaufruf-Operator (), auch Funktor genannt.
Der Index-Operator bietet sich eigentlich immer dann an, wenn die zugrunde liegende Klasse den Charakter von etwas „indizierbarem” hat.
Dies trifft auf die Klasse Polynom eigentlich nicht zu, daher ist meine Wahl auf den Funktionsaufruf-Operator () gefallen (Tabelle 7):
| Element | Beschreibung |
|---|---|
Operator () |
double operator() (double x);Auswertung des Polynoms an der Stelle x. |
Tabelle 7: Funktionsaufruf-Operator () zum Auswerten eines Polynoms.
Beispiel:
Polynom p1{ 1.0 };
std::cout << "p1: " << p1 << std::endl;
std::cout << "p1(0.0) = " << p1(0.0) << std::endl;
std::cout << "p1(1.0) = " << p1(1.0) << std::endl;
std::cout << "p1(2.0) = " << p1(2.0) << std::endl;
Polynom p2{ 1.0, 3.0 };
std::cout << "p2: " << p2 << std::endl;
std::cout << "p2(0.0) = " << p2(0.0) << std::endl;
std::cout << "p2(1.0) = " << p2(1.0) << std::endl;
std::cout << "p2(2.0) = " << p2(2.0) << std::endl;
Polynom p3{ 2.0, -4.0, 0.0, 3.0 };
std::cout << "p3: " << p3 << std::endl;
std::cout << "p3(0.0) = " << p3(0.0) << std::endl;
std::cout << "p3(1.0) = " << p3(1.0) << std::endl;
std::cout << "p3(2.0) = " << p3(2.0) << std::endl;
Ausgabe:
p1: 1
p1(0.0) = 1
p1(1.0) = 1
p1(2.0) = 1
p2: 3x^1+1
p2(0.0) = 1
p2(1.0) = 4
p2(2.0) = 7
p3: 3x^3-4x^1+2
p3(0.0) = 2
p3(1.0) = 1
p3(2.0) = 18
Natürlich lassen sich Polynome auch vergleichen. In Tabelle 8 finden Sie die üblichen Vergleichsoperatoren vor:
| Element | Beschreibung |
|---|---|
Operator == |
friend Polynom& operator== (const Polynom&, const Polynom&);Test auf Gleichheit zweier Polynome. |
Operator != |
friend Polynom& operator!= (const Polynom&, const Polynom&);Test auf Ungleichheit zweier Polynome. |
Operator < |
friend Polynom& operator< (const Polynom&, const Polynom&);Test auf „Kleiner” zweier Polynome. |
Operator <= |
friend Polynom& operator<= (const Polynom&, const Polynom&);Test auf „Kleiner-Gleich” zweier Polynome. |
Operator > |
friend Polynom& operator> (const Polynom&, const Polynom&);Test auf „Größer” zweier Polynome. |
Operator >= |
friend Polynom& operator>= (const Polynom&, const Polynom&);Test auf „Größer-Gleich” zweier Polynome. |
Tabelle 8: Vergleichsoperatoren für Objekte der Klasse Polynom.
Wir überprüfen die Vergleichsoperatoren ebenfalls an einem Beispiel:
Beispiel:
Polynom p1{ 2.0, -4.0, 0.0, 3.0 };
Polynom p2{ 3.0, 3.0, 5.0 };
std::cout << "p1: " << p1 << std::endl;
std::cout << "p2: " << p2 << std::endl;
std::cout << "p1 == p2: " << (p1 == p2) << std::endl;
std::cout << "p1 != p2: " << (p1 != p2) << std::endl;
std::cout << "p1 < p2: " << (p1 < p2) << std::endl;
std::cout << "p1 <= p2: " << (p1 <= p2) << std::endl;
std::cout << "p1 > p2: " << (p1 > p2) << std::endl;
std::cout << "p1 >= p2: " << (p1 >= p2) << std::endl;
Ausgabe:
p1: 3x^3-4x^1+2
p2: 5x^2+3x^1+3
p1 == p2: 0
p1 != p2: 1
p1 < p2: 0
p1 <= p2: 0
p1 > p2: 1
p1 >= p2: 1
Lösung
Quellcode: Siehe auch Github.
Für die Ablage der Koeffizienten in einem Polynom-Objekt gibt es mehrere Möglichkeiten.
Mit einem Objekt des Typs std::vector<double> vereinfacht sich die Implementierung der einzelnen Polynomfunktionen erheblich.
Das Grundgerüst der Klassendefinition finden Sie in Listing 1 vor:
01: class Polynom
02: {
03: private:
04: std::vector<double> m_coefficients{ 0 }; // zero polynom
05:
06: public:
07: // c'tors
08: Polynom() = default;
09: Polynom(std::initializer_list<double>);
10:
11: private:
12: // internal helper c'tor
13: Polynom(const std::vector<double>&);
14:
15: public:
16: // getter
17: size_t rank() const;
18: bool zero() const;
19:
20: // unary mathematical operators
21: friend Polynom operator+ (const Polynom&);
22: friend Polynom operator- (const Polynom&);
23:
24: // binary mathematical operators
25: friend Polynom operator+ (const Polynom&, const Polynom&);
26: friend Polynom operator- (const Polynom&, const Polynom&);
27: friend Polynom operator* (const Polynom&, const Polynom&);
28: friend Polynom operator/ (const Polynom&, const Polynom&);
29: friend Polynom operator% (const Polynom&, const Polynom&);
30:
31: // binary mathematical assignment operators
32: friend Polynom& operator+= (Polynom&, const Polynom&);
33: friend Polynom& operator-= (Polynom&, const Polynom&);
34: friend Polynom& operator*= (Polynom&, const Polynom&);
35: friend Polynom& operator/= (Polynom&, const Polynom&);
36: friend Polynom& operator%= (Polynom&, const Polynom&);
37:
38: // comparison operators
39: friend bool operator== (const Polynom&, const Polynom&);
40: friend bool operator!= (const Polynom&, const Polynom&);
41: friend bool operator< (const Polynom&, const Polynom&);
42: friend bool operator<= (const Polynom&, const Polynom&);
43: friend bool operator> (const Polynom&, const Polynom&);
44: friend bool operator>= (const Polynom&, const Polynom&);
45:
46: // functor operator
47: double operator() (double);
48:
49: // output
50: friend std::ostream& operator<< (std::ostream&, const Polynom&);
51:
52: private:
53: // private helper operators
54: friend Polynom operator* (const Polynom&, double);
55: friend Polynom operator* (double, const Polynom&);
56:
57: // horner scheme
58: double computeHorner(double) const;
59:
60: // private helper methods
61: void multiplyX(size_t);
62: void removeTrailingZeros();
63: };
Listing 1: Klasse Polynom: Definition.
Da die Klasse Polynom nur eine einzige Instanzvariable besitzt (m_coefficients vom Typ std::vector<double>, Zeile 4 von Listing 1),
bedarf diese Festlegung einiger Ergänzungen. Etliche Methoden erwarten, dass in diesem Objekt die Koeffizienten des Polynoms abgelegt sind.
Vor allem geht es darum, dass keine überflüssigen Elemente – damit sind 0-Elemente am Ende des Objekts gemeint – vorhanden sind.
Überflüssige 0-Elemente in einem std::vector<double>-Objeket würden dazu führen, dass die size()-Methode beispielsweise
einen falschen Wert zurückliefert, wenn die Anzahl der Koeffizienten gefragt ist. Natürlich ließe sich dieser Umstand auch anders lösen,
zum Beispiel dadurch, dass man neben dem m_coefficients-Objekt eine zweite Instanzvariable, nennen wir sie m_size,
mitführt und -verwaltet. Damit würden 0-Elemente am Ende des std::vector<double>-Objekts nicht zu falschen Konsequenzen führen.
„Viele Wege führen nach Rom” – bei mir ist dies die Entscheidung für einen minimalistischen Ansatz
mit einer einzigen Instanzvariablen. Dies hat allerdings zur Folge, dass eine Methode removeTrailingZeros ins Spiel kommt (Zeile 62, Listing 1),
die immer, wenn ein neues std::vector<double> berechnet wurde (nach einer Polynom-Addition, -Subtraktion etc.),
auf das Koeffizienten-Objekt angewendet wird.
Damit stellen wir in Listing 2 die Konstruktoren und die getter-Methoden rank und zero vor,
auf die removeTrailingZeros-Hilfsmethode kommen wir weiter unten noch zu sprechen:
01: // c'tors
02: Polynom::Polynom(const std::vector<double>& vector) : m_coefficients{ vector }
03: {
04: removeTrailingZeros();
05: }
06:
07: Polynom::Polynom(std::initializer_list<double> list) : m_coefficients{ list }
08: {
09: removeTrailingZeros();
10: }
11:
12: // getter
13: size_t Polynom::rank() const
14: {
15: return m_coefficients.size() - 1;
16: }
17:
18: bool Polynom::zero() const
19: {
20: return m_coefficients.size() == 1 && m_coefficients[0] == 0;
21: }
Listing 2: Klasse Polynom: Konstruktoren und getter-Methoden.
In Listing 2 finden wir zwei sehr ähnliche Konstruktoren vor:
Polynom(std::initializer_list<double> list) : m_coefficients{ list }
Polynom(const std::vector<double>& vector) : m_coefficients{ vector }
Der erste der beiden Konstruktoren ist für den Anwender gedacht – die Koeffizienten eines Polynoms lassen sich ideal
als variabel lange Liste von double-Werten übergeben. Der zweite Konstruktor ist private deklariert, er spielt in der Realisierung
der arithmetischen Operatoren eine Rolle, wenn zu einer mathematischen Operation ein Resultat-Koeffizientenvektor zu berechnen ist.
Damit wären wir schon bei der Mathematik angekommen, die Implementierung der mathematischen Operatoren finden Sie in Listing 3 vor:
001: // unary mathematical operators + and -
002: Polynom operator+ (const Polynom& p)
003: {
004: return Polynom{ p };
005: }
006:
007: Polynom operator- (const Polynom& p)
008: {
009: std::vector<double> tmp{ p.m_coefficients };
010:
011: std::for_each(std::begin(tmp), std::end(tmp), [](double& coeff) {
012: coeff *= -1.0;
013: }
014: );
015:
016: return { tmp };
017: }
018:
019: // binary mathematical operators +, -, *, / and %
020: Polynom operator+ (const Polynom& p1, const Polynom& p2)
021: {
022: size_t count = (p1.m_coefficients.size() <= p2.m_coefficients.size())
023: ? p2.m_coefficients.size()
024: : p1.m_coefficients.size();
025:
026: // create array for new coefficients
027: std::vector<double> coefficients(count);
028: for (size_t i = count - 1; i != static_cast<size_t>(-1); i--) {
029: double coeff = 0.0;
030: if (i < p1.m_coefficients.size())
031: coeff += p1.m_coefficients[i];
032: if (i < p2.m_coefficients.size())
033: coeff += p2.m_coefficients[i];
034: coefficients.at(i) = coeff;
035: }
036:
037: return { coefficients };
038: }
039:
040: Polynom operator- (const Polynom& p1, const Polynom& p2)
041: {
042: return p1 + -p2;
043: }
044:
045: Polynom operator* (const Polynom& p1, const Polynom& p2)
046: {
047: // create array of coefficients
048: size_t count = p1.m_coefficients.size() + p2.m_coefficients.size() - 1;
049:
050: // create vector of a specific size for new coefficients
051: std::vector<double> coefficients(count, 0);
052:
053: // compute coefficients of polynom product
054: for (size_t i = p1.m_coefficients.size() - 1; i != static_cast<size_t>(-1); i--) {
055: for (size_t j = p2.m_coefficients.size() - 1; j != static_cast<size_t>(-1); j--) {
056: coefficients[i + j] += p1.m_coefficients[i] * p2.m_coefficients[j];
057: }
058: }
059:
060: return { coefficients };
061: }
062:
063: Polynom operator/ (const Polynom& p1, const Polynom& p2)
064: {
065: // degree of numerator polynom is less than degree of denominator polynom
066: if (p1.m_coefficients.size() < p2.m_coefficients.size())
067: return {};
068:
069: // need copies of arguments
070: Polynom tmp1{ p1 };
071: Polynom tmp2{ p2 };
072:
073: // create coefficients array of result polynom
074: size_t count = p1.m_coefficients.size() - p2.m_coefficients.size() + 1;
075: std::vector<double> rescoeff(count);
076:
077: // apply algorithm of polynom division
078: for (size_t i = count - 1; i != static_cast<size_t>(-1); i--) {
079:
080: // premature end of division reached (comparing degrees)
081: if (tmp1.m_coefficients.size() < p2.m_coefficients.size())
082: break;
083:
084: // calculate next coefficient of result polynom
085: double coeff =
086: tmp1.m_coefficients[tmp1.m_coefficients.size() - 1] /
087: tmp2.m_coefficients[tmp2.m_coefficients.size() - 1];
088:
089: // multiply denominator polynom with coefficient
090: tmp2 = tmp2 * coeff;
091:
092: // calculate difference of ranks
093: size_t diffRank = tmp1.m_coefficients.size() - p2.m_coefficients.size();
094:
095: // multiply denominator polynom with one ore more 'x'
096: tmp2.multiplyX(diffRank);
097:
098: // subtract denominator polynom from numerator polynom
099: tmp1 = tmp1 - tmp2;
100:
101: // poke calculated coefficient into result polynom
102: rescoeff[diffRank] = coeff;
103:
104: // restore denominator polynom
105: tmp2 = p2;
106: }
107:
108: return { rescoeff };
109: }
110:
111: Polynom operator% (const Polynom& p1, const Polynom& p2)
112: {
113: return p1 - (p1 / p2) * p2;
114: }
Listing 3: Klasse Polynom: Arithmetische Operatoren (binär und unär).
Die Realisierung der arithmetischen Operatoren in Listing 3
hält sich streng an die vorgestellten Algorithmen. Da wir es häufig mit Wiederholungsschleifen
in Zusammenspiel mit dem Datentyp size_t zu tun haben, sollten wir auf eine mögliche Stolperfalle näher eingehen:
Wie traversiere ich eine Wiederholungsschleife korrekt rückwärts?
Wir könnten es auf die folgende Weise versuchen:
for (size_t i = m_coefficients.size()-1; i >= 0; --i){
// do something with m_coefficients[i]
}
Dieses Code-Fragment enthält einen schwerwiegenden Fehler: Da der Schleifenzähler i ein Typ ohne Vorzeichen ist,
wird i niemals kleiner als 0 sein! Aus diesem Grund haben wir es hier mit einer Endlosschleife zu tun!
Eine mögliche korrekte Variante sieht so aus:
for (size_t i = m_coefficients.size()-1; i != static_cast<size_t>(-1); --i){
// do something with m_coefficients[i]
}
Da i ein Typ ohne Vorzeichen ist, wird i-1, wenn i gleich 0 ist, zu static_cast<size_t>(-1).
Auf diese stoppt die Schleife korrekt.
Nebenbemerkung: i-1 ist der größte Wert, den eine Variable des Typs size_t darstellen kann.
Die Realisierung des Horner-Schemas birgt keine Schwierigkeiten. Natürlich hätte man in der Realisierung (Listing 4)
auch eine simple klassische for-Wiederholungsschleife einsetzen können. Ich wollte im gesamten Programm
so viel wie möglich und sinnvoll Algorithmen der STL arbeiten,
um auf diese Weise ihren Umgang zu schulen. Beachten Sie mehrere Kleinigkeiten in Listing 4:
Zum einen müssen wir den Koeffizienten-Vektor rückwärts traversieren, es kommen deshalb die beiden Iteratoren-Objekte zum Einsatz,
die wir mit einem Aufruf von std::rbegin() und std::rend() erhalten.
Des weiteren starten wir das Horner-Schema nicht mit dem ersten Koeffizienten,
sondern innerhalb der Wiederholungsschleife mit dem zweiten (der erste Koeffizient wird in Zeile 5 berücksichtigt).
Dies erklärt den Aufruf von std::next() in Zeile 8 von Listing 4:
01: // horner scheme
02: double Polynom::computeHorner(double x) const
03: {
04: size_t count = m_coefficients.size();
05: double y = m_coefficients[count - 1];
06:
07: std::for_each(
08: std::next(std::rbegin(m_coefficients)),
09: std::rend(m_coefficients),
10: [&](double coeff) {
11: y = coeff + y * x;
12: }
13: );
14:
15: return y;
16: }
17:
18: // apply horner scheme, using functor operator
19: double Polynom::operator() (double x)
20: {
21: return computeHorner(x);
22: }
Listing 4: Klasse Polynom: Realisierung des Horner-Schemas.
Das (wiederholte) Multiplizieren eines Polynoms mit x – so wie dies an manchen Stellen in der Implementierung der arithmetischen
Operatoren benötigt wird – übernimmt die Hilfsmethode multiplyX (Listing 5).
Wiederum mit Hilfe eines geschickt gewählten STL-Algorithmus ist diese Implementierung sehr einfach,
wenngleich möglicherweise ein klein wenig trickreich ausgefallen:
01: void Polynom::multiplyX(size_t k)
02: {
03: // create new array of coefficients
04: std::vector<double> tmp(m_coefficients.size() + k);
05:
06: // compute new coefficients - same as shifting to the right
07: std::move(m_coefficients.begin(), m_coefficients.end(), tmp.begin() + k);
08:
09: // switch coefficients buffer
10: m_coefficients = tmp;
11: }
Listing 5: Klasse Polynom: Realisierung der multiplyX-Methode.
Der Aufruf der Methode std::move in Zeile 7 von Listing 5 ist nicht zu verwechseln mit der gleichnamigen Methode aus dem
Standard Library Header <utility> (hier fungiert std::move() als eine Umwandlungsfunktion,
die aus dem Argument eine RValue-Referenz erzeugt).
Es gibt eine weitere Überladung der Methode im Standard Library Header <algorithm>, die eine Verschiebung von Elementen in einem
Bereich vollzieht. Dies ist in Zeile 7 von Listing 5 der Fall, der Bereich ist ein std::vector<double>-Objekt,
das in Zeile 4 mit einer bestimmten Länge angelegt und mit 0-Werten vorbelegt wird.
Und noch zwei weitere STL-Algorithmen können wir in Aktion betrachten (Listing 6): std::transform und std::find_if.
Wir sind bei Methode removeTrailingZeros und bei einer Überladung des operator*-Operators angekommen:
01: // private helper operators
02: Polynom operator* (double scalar, const Polynom& p)
03: {
04: // scalar multiplication with STL
05: Polynom q{ p };
06: std::transform (
07: std::begin(p.m_coefficients),
08: std::end(p.m_coefficients),
09: std::begin(q.m_coefficients),
10: [scalar](const auto& elem) {
11: return elem * scalar;
12: }
13: );
14: return q;
15: }
16:
17: void Polynom::removeTrailingZeros()
18: {
19: // remove trailing zeros, if any ... using STL algorithms
20: std::reverse_iterator<std::vector<double>::iterator> r_it = std::find_if(
21: std::rbegin(m_coefficients),
22: std::rend(m_coefficients),
23: [](double value) { return value != 0.0; }
24: );
25:
26: // vector contains only '0's - rescue last '0'
27: if (r_it == std::rend(m_coefficients)) {
28: r_it--;
29: }
30:
31: m_coefficients.erase(r_it.base(), std::end(m_coefficients));
32: }
Listing 6: Klasse Polynom: Anwendung der beiden STL-Algorithmen std::transform und std::find_if.
Die std::transform-Methode in Zeile 6 von Listing 6 verwenden wir, um ein Polynom mit einem skalaren Wert zu multiplizieren.
Im Prinzip legen wir vom Ausgangspolynom eine Kopie an, die std::transform-Methode arbeitet auf der Kopie und multipliziert
jeden einzelnen Koeffizienten mit einem Skalar. Die std::find_if-Funktion wiederum setzen wir ein,
um mögliche 0-Elemente am Ende des Koeffizientenvektors zu suchen. Da es in einem Sonderfall ein zulässiges 0-Element am
Ende des Vektors geben darf (Null-Polynom), schließen wir diesen Fall in den Zeilen 26 bis 29 aus.
Das Löschen der Elemente schließlich übergeben wir der Methode erase() am std::vector<double>-Objekt.
Hinweis: Zeile 20 von Listing 6 könnte man leichter lesbarer formulieren:
auto r_it = std::find_if (
...
Ich überlasse es Ihrer Entscheidung, welchen Programmierstil Sie bevorzugen: Einfache Lesbarkeit des Quellcodes versus präzise Formulierungen der zum Einsatz kommenden Datentypen. Leider ist es nicht immer möglich, beides unter einen Hut zu bringen. Mit diesen Erläuterungen sollten die wesentichen Passagen des Quellcodes angesprochen worden sein, die noch fehlenden Programmteile finden Sie hier vor.
There‘s more
Unsere bisherigen Betrachtungen haben sich ausschließlich auf Polynome mit Koeffizienten des Typs double beschränkt.
Mittlerweile unterstützt C++ drei Gleitkommadatentypen:
float– Gleitkommatyp mit einfacher Genauigkeit.double– Gleitkommatyp mit doppelter Genauigkeit.long double– Gleitkommatyp mit erweiterter doppelter Genauigkeit.
Welche Änderungen sind an der Klasse Polynom vorzunehmen,
um Polynome mit unterschiedlichen Gleitkommadatentypen definieren zu können?
There‘s much more
In C++ 20 wird ein neues Sprachkonzept – genannt Concepts – eingeführt. Mit Concepts kann man Restriktionen für Datentypen festzulegen, die eine Template-Funktion oder -klasse annehmen kann.
Definieren Sie Ihre Klasse Polynom<T> mit Hilfe von Concepts so, dass ausschließlich die drei Datentypen
float, double und long double als Template-Argument in Betracht kommen!