Das Springerproblem ist auf den Schweizer Mathematiker Leonhard Euler (1707 – 1783) zurückzuführen. Dieser stellte sich vor über 200 Jahren, genauer gesagt im Jahre 1758, die folgende Frage: „Gegeben sei ein leeres Schachbrett. Gibt es eine Zugfolge, mit der der Springer alle (schwarzen und weißen) Felder des Bretts genau einmal besucht?”.
Hmmm, eine gute Frage, wird sich der geneigte Leser jetzt sagen. Möglicherweise kann man sie innerhalb von wenigen Minuten selbst beantworten, schließlich ist ein Schachbrett mit seinen 8×8 Feldern nicht so wirklich groß. Stellt man nach einer ersten Phase euphorischen Suchens ernüchternd fest, dass das Problem doch nicht ganz so einfach zu lösen ist, kommt man vielleicht auf den revolutionären Gedanken, dem Problem mit Hilfe eines Softwareprogramms auf den Leib zu rücken. Dies ist natürlich möglich, wie wir in dieser Fallstudie am Beispiel von Modern C++ zeigen werden.
Neben der Implementierung einer Backtracking-Strategie betrachten wir auch Überlegungen,
wie sich das Suchen von Zugfolgen parallelisieren lässt.
Die Methode std::async und Objekte, die es „erst in der Zukunft” gibt (std::future<T>), kommen zum Einsatz.
Lernziele
- Einheitliche Initialisierung und Default-Initialisierung
- Einheitliche Initialisierung mit redundanten Typnamen
- STL-Containerklassen
std::list<T>,std::vector<T>,std::array<T>undstd::deque<T> - STL-Algorithmus
std::for_each if-Anweisung mit Variablen-Initialisierung- Parallelverarbeitung mit
std::future<T>undstd::async - Schlüsselwort
auto - Datentyp
size_t if constexprzur Übersetzungszeit- Schlüsselwort
noexcept
Einführung
Der Standardalgorithmus für die Lösung solcher Probleme ist das sogenannte Backtracking. Dabei legen wir zugrunde, dass der Springer auf dem Schachbrett in der Ecke unten links startet. Die Idee hierbei ist, die Figur solange zu setzen, bis entweder eine Lösung gefunden wurde, oder man sie nicht mehr weitersetzen kann. In diesem Fall geht man dann einen Zug zurück und versucht, eine Lösung über einen alternativen Weg zu finden. Auf diese Weise findet das Verfahren immer eine oder mehrere Lösungen – wenn es sie denn gibt.
Zu beachten ist dabei leider noch ein kleiner Schönheitsfehler: Die Laufzeiten derartiger Programme können immens sein (Tage, Wochen, Jahre, …), je nachdem, welche Schachbretter wir betrachten, wenn wir das Springerproblem nicht nur für Schachbretter mit der Standardgröße von 8×8 Feldern analysieren wollen, sondern verallgemeinert betrachten.
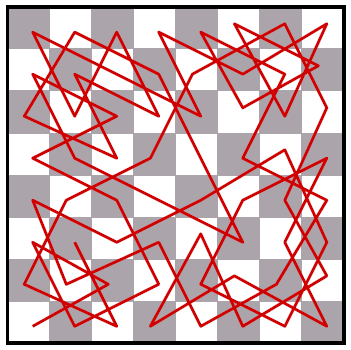
Prinzipiell ist von vorneherein nicht klar, ob es überhaupt eine Lösung gibt. Wenn ja, kann es auch sein, dass mehrere Zugfolgen existieren! Eine mögliche Lösung des Springerproblems auf einem realen Schachbrett (also mit 64 Feldern) finden Sie in Abbildung 1 vor:
Abbildung 1: Eine Lösung des Springerproblems für ein 8×8 Schachbrett.
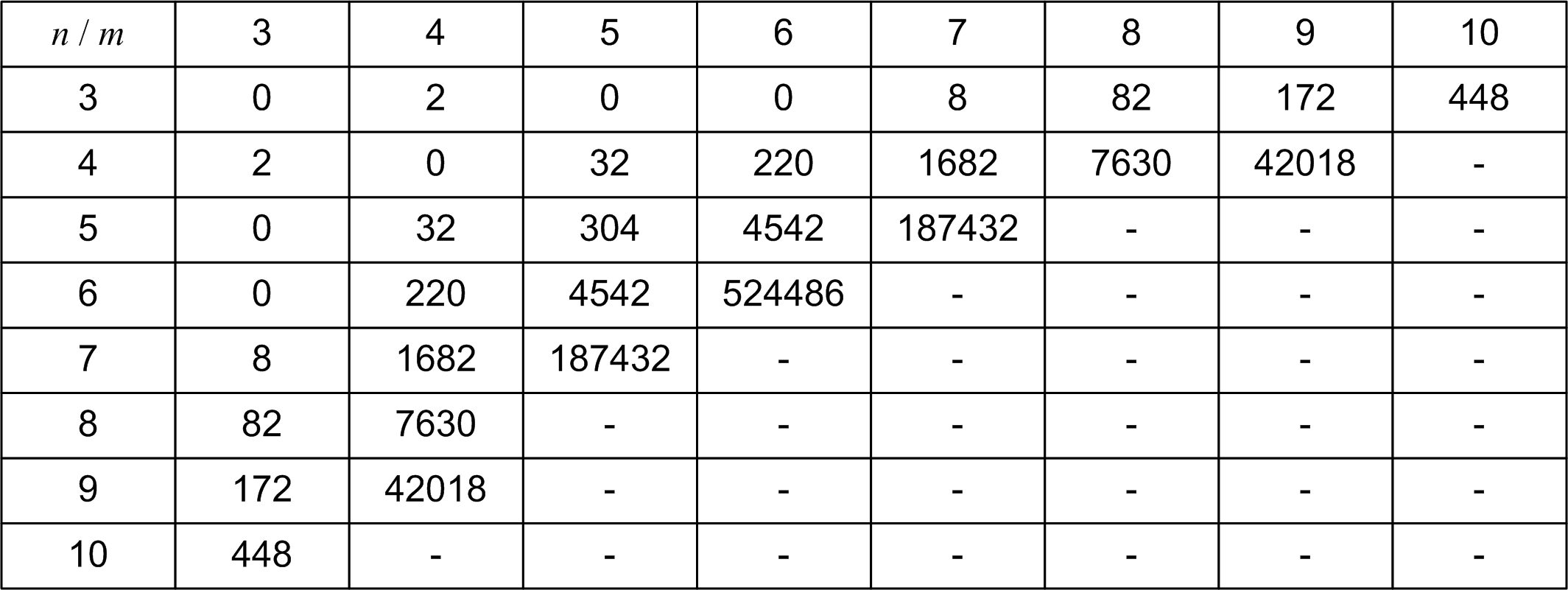
Mit den Rechnern der aktuellen Generation wird es sehr schwer sein, für ein 8×8 Schachbrett alle Lösungen zu bestimmen. Wir konzentrieren uns deshalb in der Aufgabe auf kleinere Bretter. Die Anzahl realistisch ermittelbarer Lösungen für derartige Schachbretter können Sie Abbildung 2 entnehmen:
Abbildung 2: Einige Resultate des Springerproblems.
Damit kommen wir jetzt auf die Details des Springerproblems zu sprechen. Die Zugregel für einen Springer kann man so beschreiben: Von einem Ausgangsfeld kann dieser zuerst zwei Felder in eine beliebige Richtung gehen (keine Diagonale) und dann noch ein Feld zur Seite treten. Befindet er sich in einem der mittleren Felder des Spielfeldes, so gibt es 8 Zielfelder, die er betreten könnte (siehe dazu auch Abbildung 3). Steht er hingegen mehr in der Nähe des Schachbrettrands, so verringert sich die Anzahl der Sprungmöglichkeiten entsprechend.
Abbildung 3: Zugmöglichkeiten des Springers auf einem Schachbrett.
Lösungsstrategie „Trial and Error”
Wir erläutern nun eine Lösungsstrategie für das Springerproblem am Beispiel eines 3×4-Schachbretts und erklären in einzelnen Schritten den Ablauf. Exemplarisch legen wir für den Springer die Startposition in der linken unteren Ecke fest, also das Feld mit den Koordinaten (2,0), wobei wir den Ursprung des Bretts in der linken, oberen Ecke festlegen ( Abbildung 4). Es wäre aber auch jedes andere Feld zur Erörterung der Lösungsstrategie geeignet. Die „1” symbolisiert, dass es sich um den ersten Zug des Springers handelt:
Abbildung 4: Ausgangssituation „1”: Springer wird im linken unteren Feld platziert.
Anhand der Ausgangsposition des Springers bestimmen wir nun eine Liste seiner möglichen Züge, die er von der aktuellen Position aus bestreiten kann. Sitzt der Springer auf dem Feld (2,0), so hat er in diesem Fall die Wahl zwischen zwei Zielfeldern (0,1) und (1,2), um weiter voran zu schreiten. Sie finden diese Felder in Abbildung 5 grau hinterlegt vor. Wir entscheiden uns für das erste Feld aus der Liste, auf dem Schachbrett nehmen wir durch die „2” eine entsprechende Nummerierung vor:
Abbildung 5: Spielsituation „2”: Springer zieht von Feld (2,0) nach Feld (0,1).
Von der aktuellen Springerposition ausgehend bestimmen wir wieder alle möglichen Felder, auf die der Springer nun springen kann. Es ist wieder eine Liste mit zufälligerweise zwei Positionen, dieses Mal sind es die Felder (1,3) und (2,2), siehe Abbildung 6. Wir wählen wieder das erste Element aus der Liste aus und setzen die Figur auf das Feld (1,3):
Abbildung 6: Spielsituation „3”: Springer zieht von Feld (0,1) nach Feld (1,3).
Es wurden bei weitem noch nicht alle Felder des Schachbretts besucht. Von der Springerposition (1,3) ausgehend bietet sich dieses Mal aber nur ein einziges Feld (2,1) für den Folgezug an, siehe Abbildung 7:
Abbildung 7: Spielsituation „4”: Springer zieht von Feld (1,3) nach Feld (2,1).
Und noch einmal gilt es diese Runde zu drehen. Dieses Mal können wir zwei Felder (0,0) und (0,2) als mögliche nächste Kandidaten ausmachen. Wir entscheiden uns in Abbildung 8 für das Feld (0,0):
Abbildung 8: Spielsituation „5”: Springer zieht von Feld (2,1) nach Feld (0,0).
Ich verspreche es, diese Runde drehen wir jetzt zum letzten Mal. Es gibt wieder nur ein einziges Feld zum Weiterspielen, in Abbildung 9 erkennen Sie das weitere Vorgehen:
Abbildung 9: Spielsituation „6”: Springer zieht von Feld (0,0) nach Feld (1,2).
Wir sind an einer entscheidenden Stelle in der Betrachtung der Lösungsstrategie angekommen. Wenn Sie Abbildung 9 betrachten, werden Sie erkennen, dass es von der aktuellen Springerposition aus betrachtet keine weitere Möglichkeit gibt, zu springen und damit zu einer Lösung des Springerproblems zu gelangen. Jetzt kommen die Listen mit den möglichen Folgezügen aus den vorherigen Schritten zum Zuge. Offensichtlich war die Auswahl eines Folgezugs in den Schritten zuvor nicht Erfolg versprechend. Wir müssen die Figur also auf die vorherige Ausgangssituation zurücksetzen. Da wir in diesem Schritt (im konkret vorliegenden Beispiel) aber nur einen einzigen Folgezug hatten, müssen wir gleich noch eine weitere Ausgangssituation zurücksetzen und kommen damit in Abbildung 7 an. Dort hatten wir, vom Spielfeld mit der Nummer 4 ausgehend, die zwei möglichen Folgezüge (0,0) und (0,2) zur Auswahl. Die Entscheidung für (0,0) hat nicht zum Ziel geführt, also versuchen wir es jetzt mit der zweiten Alternative (0,2), siehe Abbildung 10. Sie verstehen jetzt, zu welchem Zweck die Listen mit den möglichen Folgezügen aufzubewahren sind. Gelangt man in einem bestimmten Schritt in die missliche Situation, dass es keine Folgezüge mehr gibt, muss man einen oder mehrere Schritte rückgängig machen und mit einem alternativen Folgezug sein Glück von Neuem versuchen.
Abbildung 10: Springer geht zur Spielsituation „4” zurück und springt jetzt von (2,1) nach Feld (0,2).
Dieses Verfahren läuft solange weiter, bis alle Felder des Schachbrettes besucht worden sind (und man damit eine Lösung gefunden hat), oder man eben feststellt, dass es keine Lösung gibt. Möchte man alle Lösungen zu einer bestimmten Schachbrettgröße finden, bricht man das Verfahren nach dem Entdecken einer Lösung nicht ab, sondern hinterlegt die gefundene Lösung in einer geeigneten Datenstruktur und setzt das Verfahren mit den noch vorhandenen Alternativzügen fort. Wenn Sie alles richtig gemacht haben, werden Sie bei dem betrachteten Beispiel eines 3×4-Schachbretts zwei Lösungen aufspüren, die Sie in Abbildung 11 betrachten können:
Abbildung 11: Zwei Lösungen des Springerproblems auf einem 3×4-Schachbrett.
Die dargelegte Lösungsstrategie ist in der Informatik unter dem Begriff „Trial and Error” geläufig. Sie findet immer dann Anwendung, wenn zur Lösung eines Problems kein systematisches Verfahren zur Verfügung steht. Bei der „Trial and Error”-Methode werden nacheinander alle in Frage kommenden Lösungskandidaten durchprobiert, bis eine oder mehrere Lösungen gefunden wurden.
Im Falle des Springerproblems bedeutet dies, dass nach dem Setzen des Springers auf ein Ausgangsfeld maximal 8 Möglichkeiten zu betrachten sind, um auf das nächste Feld zu springen. Auf diesem Feld gibt es wiederum maximal 8 Möglichkeiten, um zum nächsten Feld weiterzuziehen usw. Geht es auf einem bestimmten Spielfeld überhaupt nicht mehr weiter, wird der letzte Schritt (beziehungsweise die letzten Schritte) zurückgenommen, und es werden stattdessen alternative Zugmöglichkeiten ausprobiert. Hieraus erklärt sich auch der Begriff „Backtracking”, der häufig bei „Trial and Error”-Problemen anzutreffen ist.
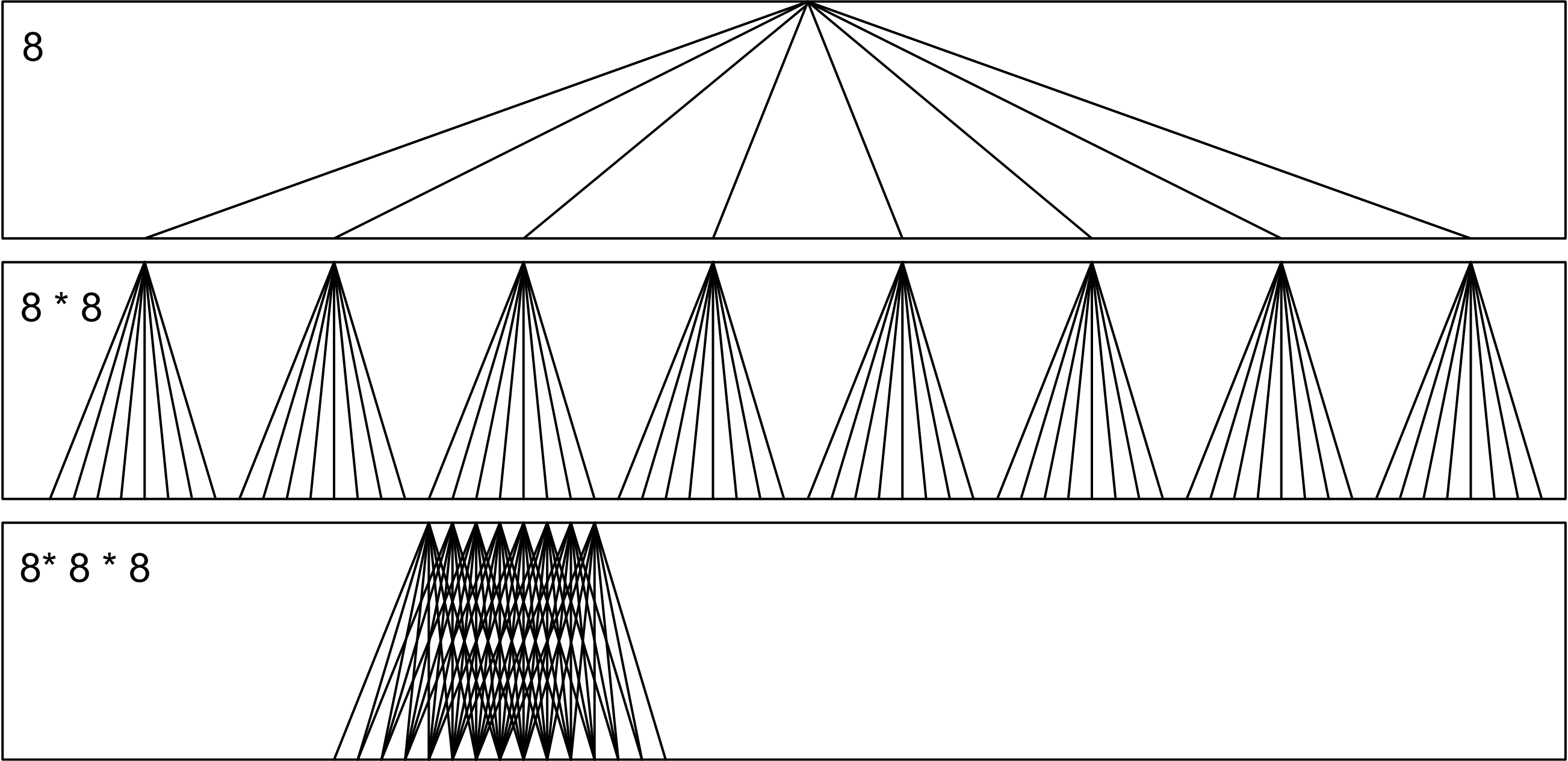
Durch das systematische Vorwärts- und Rückwärtsziehen des Springers auf dem Schachbrett ist sichergestellt, dass alle in Frage kommenden Lösungswege betrachtet werden. Bildlich gesprochen kann man die Bewegungen des Springers als „Aufspannen eines Lösungsbaums” ansehen (Abbildung 12). In diesem Baum gilt es, Ast für Ast zu traversieren, um die Lösungen zu finden. Führt ein Ast nicht zu einer Lösung, so muss man auf diesem Ast zurückgehen und einen anderen Ast überprüfen.
Abbildung 12: Lösungsbaum eines Backtracking-Verfahrens.
In der programmiersprachlichen Umsetzung müssen wir den Lösungsbaum nicht explizit erzeugen. Backtracking-Verfahren lassen sich typischerweise am einfachsten rekursiv beschreiben, die Möglichkeit eines rekursiven Methodenaufrufs nimmt einem diese Arbeit quasi ab, oder noch verwirrender: Der Lösungsbaum wird auf dem Methodenaufrufstapel implizit, quasi versteckt aufgespannt.
In unserem konkreten Beispiel lässt sich nun zusammenfassend das Lösungsverfahren durch die in Abbildung 13 skizzierte, rekursive Methode findMoves darstellen:
Methode:
findMoves
Eingabe: Aktuelle Position (x, y) des Springers
- Springer setzen: Markiere Zielfeld (x, y) als belegt
- if („alle Felder des Schachbretts sind belegt„) then
Lösung gefunden: In Liste abspeichern- else
* Bestimmung aller möglichen Folgezüge des Springers
* Für alle möglichen Folgezüge (x', y'):
Aufruf vonfindMovesmit (x', y') // Rekursion- endif
- Springer zurücksetzen: Markiere Zielfeld (x, y) als unbelegt // Backtracking
Abbildung 13: Grobskizze einer rekursiven Methode findMoves zur Bestimmung aller Zugfolgen.
Wir schließen die theoretischen Vorarbeiten hiermit ab, es folgen Hinweise für eine Umsetzung des Lösungsverfahrens in eine Modern C++-Anwendung.
Klasse Coordinate
Für die Koordinaten des Schachbretts verwenden wir eine Klasse Coordinate, um zwei ganzzahlige Werte x und y, die eine Position auf dem Schachbrett beschreiben, zu kapseln. Dafür gäbe es natürlich in C++ mehrere Möglichkeiten, eine von ihnen wäre der Einsatz der STL-Klasse std::pair<T>. Ich habe mich für eine rudimentäre C++-Klasse Coordinate entschieden, deren Definition Sie Tabelle 1 entnehmen können:
| Element | Beschreibung |
|---|---|
| Konstruktor | Coordinate();Es wird die Koordinate {0, 0} erzeugt. |
| Benutzerdefinierter Konstruktor | Coordinate(int row, int col);Es wird die Koordinate mit Reihe row und Spalte col erzeugt. |
getter getRow() |
int getRow();Liefert die Reihe der Koordinate zurück. |
getter getCol() |
int getCol();Liefert die Spalte der Koordinate zurück. |
Methode fromOffset() |
Coordinate<T> fromOffset(int rowOfs, int colOfs);Liefert eine neue Koordinate zurück, die sich aus der aktuellen Koordinate modifiziert um die beiden Offsets rowOfs und colOfs ergibt. |
Operator << |
friend std::ostream& operator<< (std::ostream&, const Coordinate&);Gibt ein Coordinate-Objekt auf der Konsole aus. |
Tabelle 1: Wesentliche Elemente der Klasse Coordinate.
Klasse KnightProblemBoard
Für das Schachbrett selbst definieren wir eine Klasse KnightProblemBoard. Im Großen und Ganzen kann man sagen, dass diese Klasse eine zwei-dimensionale Ausprägung eines Objekts des Typs std::array<> kapselt.
Diese Klasse bietet sich vor allem dann an, wenn die Dimension(en) des Felds bekannt und fest sind.
Mit seiner Hilfe lässt sich die Implementierung der noch ausstehenden Klasse KnightProblemSolver vereinfachen.
Ein Wert 0 im std::array<>-Objekt besagt, dass das korrespondierende Feld noch nicht vom Springer besucht wurde. Ganzzahlige Werte größer Null besagen, dass der Springer schon auf dem Feld war. Der Wert selbst gibt an, beim wievielten Zug das Feld betreten wurde:
Abbildung 12: Zweidimensionale Matrix zur Verwaltung eines 3×4 Schachbretts inklusive Springerzug.
Die Momentaufnahme des Beispiels aus Abbildung 14 besagt, dass auf dem Schachbrett bereits ein Springerzug der Länge vier stattgefunden hat. Der Algorithmus ist offenbar noch damit beschäftigt, den vorliegenden Springerzug zu einem Zug mit 12 Sprüngen zu vervollständigen. Eine gefundene Lösung spiegelt sich in dem std::array<>-Objekt also dadurch wieder, dass keine Nullen mehr vorhanden sind und jeder Wert zwischen 1 und dem Produkt der Reihen- und Spaltenanzahl genau einmal auftritt. Zwei Beispiele solcher std::array<>-Objekte hatten wir in Abbildung 11 schon gesehen.
Mit Tabelle 2 schließen wir die Betrachtung der Klasse KnightProblemBoard ab:
| Element | Beschreibung |
|---|---|
| Konstruktor | KnightProblemBoard();Es wird ein leeres Schachbrett angelegt, alle Felder sind mit 0 vorbelegt. |
getter at() |
int& at(const Coordinate<T>& coord);Liefert eine Referenz des Schachbretts an der Stelle coord zurück. |
Methode clearBoard() |
void clearBoard();Alle Felder des Schachbretts werden mit dem Wert 0 belegt. |
Operator << |
friend std::ostream& operator<< (std::ostream&, const KnightProblemBoard&);Gibt ein KnightProblemBoard-Objekt auf der Konsole aus. |
Tabelle 2: Wesentliche Elemente der Klasse KnightProblemBoard.
Klasse KnightProblemSolver
Wir kommen auf das Kernstück der Aufgabe zu sprechen. In der Klasse KnightProblemSolver wird auf Basis der Backtracking-Lösungsstrategie die Menge aller Springerproblemlösungen zu einer bestimmten Schachbrettgröße berechnet. Zunächst stellen wir in Tabelle 3 die getter-Methoden der KnightProblemSolver-Klasse vor:
| getter-Methode | Beschreibung |
|---|---|
getter getRows() |
int getRows();Liefert die Anzahl der Reihen des Schachbretts zurück. |
getter getCols() |
int getCols();Liefert die Anzahl der Spalten des Schachbretts zurück. |
getter getSolutions() |
std::list<std::list<Coordinate> getSolutions();Liefert die Liste aller ermittelten Lösungen des Springerzug-Problems zurück. Im Falle des Beispiels aus Abbildung 11 sieht die Liste am Ende des Programms so aus: 0: {2,0} {1,2} {0,0} {2,1} {1,3} {0,1} {2,2} {0,3} {1,1} {2,3} {0,2} {1,0}1: {2,0} {1,2} {0,0} {2,1} {1,3} {0,1} {2,2} {1,0} {0,2} {2,3} {1,1} {0,3}Found: 2 |
Tabelle 3: getter-Methoden der Klasse KnightProblemSolver.
Weiter geht es mit den Instanzvariablen eines KnightProblemSolver-Objekts. Im Mittelpunkt steht hier offensichtlich ein Objekt des Typs KnightProblemBoard, siehe Tabelle 2. Weitere, wichtige Instanzvariablen der KnightProblemSolver-Klasse, sofern sie durch die getter-Methoden aus Tabelle 3 nicht schon abgehandelt wurden, entnehmen Sie bitte Tabelle 4:
| Instanzvariable | Beschreibung |
|---|---|
m_board |
KnightProblemBoard m_board;Repräsentiert das Schachbrett, das durch ein KnightProblemSolver-Objekt verwaltet wird. |
m_current |
std::list<Coordinate> m_current;Liste von Coordinate-Objekten zur Ablage eines Springerzugs. Zu Beginn der Suche ist das m_current-Objekt logischerweise leer. Dem Springerzug aus Abbildung 14 entspricht das Listenobjekt{ {2,0}, {1,2}, {0,0}, {2,1} }. |
m_solutions |
std::list<std::list<Coordinate>> m_solutions;Liste der zu einem bestimmten Zeitpunkt während der Ausführung des Backtracking-Algorithmus bislang gefundenen Lösungen. |
m_moveNumber |
int m_moveNumber;Zähler für den Sprung im aktuellen Springerzug. Die Variable nimmt Werte zwischen 1 (Ausgangsposition) und Zeilenanzahl × Spaltenanzahl (letzter Zug eines Lösungszugs) an. |
Tabelle 4: Zentrale Instanzvariablen der Klasse KnightProblemSolver.
Wie findet man nun eine Folge von Springerzügen auf dem Schachbrett? Die Grobskizze der Methode findMoves aus Abbildung 13 gilt es nun zu verfeinern. Hierzu betrachten wir in Tabelle 5 zuerst alle Hilfsmethoden der Klasse KnightProblemSolver, die zur Realisierung der findMoves-Methode beitragen:
| Methode | Beschreibung |
|---|---|
setKnightMoveAt |
void setKnightMoveAt(const Coordinate& coord);Setzt den Springer auf dem Schachbrett auf die Position coord. Im m_board-Objekt sollte die Nummer des Zugs eingetragen werden. |
unsetKnightMoveAt |
void unsetKnightMoveAt(const Coordinate& coord);Macht einen Springerzug auf dem Schachbrett an der Position coord rückgängig. Im m_board-Objekt sollte der Wert 0 eingetragen werden. |
inRange |
bool inRange(const Coordinate& coord);Liefert true oder false in Abhängigkeit davon zurück, ob die Werte des Coordinate-Objekts ein gültiges Feld auf dem Schachbrett spezifizieren oder nicht. |
canMoveTo |
bool canMoveTo(const Coordinate& coord);Liefert true zurück, wenn der Springer von der aktuellen Position auf das Feld mit der Position coord springen kann. Die Koordinaten müssen gültig sein und das Feld darf von dem Springer noch nicht durch einen vorangegangenen Zug betreten worden sein. |
nextKnightMoves |
std::vector<Coordinate>nextKnightMoves(const Coordinate& coord);Erstellt eine Liste mit allen möglichen Folgezügen, ausgehend von der Position coord. Ein Springer, der auf einem Schachbrett auf dem Feld mit den Koordinaten (x,y) steht, kann im nächsten Zug die Felder mit folgenden Koordinaten erreichen (siehe dazu auch Abbildung 3):(x-1, y+2) und (x-1, y-2), (x-2 , y+1) und (x-2, y-1), (x+1, y-2) und (x+1, y+2), (x+2, y+1) und (x+2, y-1) Hierbei ist natürlich jeweils zu überprüfen, ob der Zielzug überhaupt auf dem Schachbrett liegt, siehe dazu die Methoden inRange bzw. canMoveTo. Folglich kann die Resultatliste bis zu acht Coordinate-Elemente enthalten. |
isSolution |
bool isSolution();Liefert true zurück, wenn aktuell auf dem Schachbrett eine Lösung des Springerproblems vorliegt, andernfalls false. |
Tabelle 5: Hilfsmethoden der Klasse KnightProblemSolver.
Wir sind so gut wie am Ziel angekommen. Die einzige noch fehlende Methode findMoves ist in Tabelle 6 definiert:
| Methode | Beschreibung |
|---|---|
findMoves |
int findMoves(const Coordinate& coord);Bestimmt alle Lösungen des Springerproblems, falls vorhanden. Zum Beginn der Suche ist der Springer auf die Position coord gesetzt, typischerweise die linke untere Ecke des Schachbretts. Die Lösungen sind über die getter-Methode getSolutions() verfügbar. |
Tabelle 6: Methode findMoves der Klasse KnightProblemSolver.
Hinweis: In der noch folgenden Realisierung der Klasse KnightProblemSolver werden Sie feststellen, dass an Stelle der Methode findMoves gleich zwei
Methoden findMovesSequential und findMovesParallel in Erscheinung treten. Auf die Unterschiede dieser beiden Methoden kommen wir weiter unten noch zu sprechen.
Einen Pseudo-Code der findMoves-Methode finden Sie in Abbildung 15 vor. Beachten Sie, wie die Hilfsmethoden der Klasse KnightProblemSolver aus Tabelle 4 zum Einsatz gelangen:
Methode:
findMoves
Eingabe: Aktuelle KoordinateCoordinate:coorddes Springers
- Füge Springer auf Feld
coordhinzu: Aufruf vonsetKnightMoveAt()- Füge Springerposition
coordin Listem_currenthinzu: Aufruf vonpush_back()- if (
isSolution()==true) then
Speicher Lösung inm_solutionsab: Aufruf vonnextKnightMoves()- else
* Bestimme ListenextMovesaller möglichen Folgezüge: Aufruf vonpush_back()
* for (tmpinnextMoves)
Rekursiver Aufruf:findMoves()mittmp
* endfor- endif
- Entferne Springer von Position
coord: Aufruf vonunsetKnightMoveAt()- Entferne Springer aus Liste
m_current: Aufruf vonpop_back()
Abbildung 15: Verfeinerung der rekursiven Methode findMoves zur Bestimmung aller Zugfolgen.
Parallelisierung des Algorithmus
Wie kann man die Suche nach Lösungen des Springerproblems parallelisieren? Ist der Springer erst einmal auf seinem Startfeld positioniert, können die versuchsweisen Bestimmungen der Zugfolgen von jeweils einem separaten Thread durchgeführt werden. Da jeder Versuch zur Lösung des Springerproblems sich Notizen auf dem Schachbrett macht (Eintragung der Zugnummer), benötigt jede Task ein eigenes Schachbrett. Im Vergleich zu dem zeitlichen Gewinn, der bei der Parallelisierung des Algorithmus entsteht, ist diese Anforderung an die Implementierung jedoch als äußerst marginal einzustufen.
Sie haben soeben das Master-Slave-Modell als eine Organisationsform zur Parallelisierung von Algorithmen kennen gelernt ([Abbildung 16]). Ein Master-Thread ist bei diesem Modell für die grundlegenden Aufgaben wie Organisation des Schachbretts, seine Visualisierung oder den Empfang und die Verwaltung asynchron eintreffender Lösungen zuständig. Die eigentliche Aufgabe, das Suchen nach Zugfolgen auf dem Schachbrett, wird an einen oder mehrere Slave-Threads delegiert. In Abhängigkeit von den zur Verfügung stehenden Ressourcen des Rechners entscheidet der Master-Thread, wie viele Slave-Threads zu erzeugen sind – oder auch zu einem späteren Zeitpunkt noch zusätzlich nachgestartet werden können. Alle Daten, die vom Master- und seinen Slave-Threads gemeinsam benutzt werden, dürfen natürlich nur nach der Strategie des „gegenseitigen Ausschlusses” benutzt werden.
Abbildung 16: Master-Slave-Modell als eine Organisationsform paralleler Algorithmen.
Ergänzen Sie Ihre Realisierung der Klasse KnightProblemSolver um eine Methode findMovesParallel, die parallel arbeitet. Die Startposition des Springers bleibt dabei zunächst in der linken unteren Ecke des Schachbretts. Nun berechnen Sie alle möglichen Züge, die der Springer von dieser Startposition aus tätigen kann. Damit haben Sie gleichzeitig die Anzahl der Slave-Threads gefunden, die Sie mit der parallelen Lösungssuche des Problems beauftragen können. Pro Thread ist nun eine Kopie des Schachbretts anzulegen. Auf allen Kopien wird die jeweilige Startposition des Springers vermerkt. Die nun folgenden Aufrufe der findMoves-Methode werden jeweils in den Kontext eines Slave-Threads ausgelagert. Die jeweils zweite Zugposition des Springers ist dem Thread als Parameter zu übergeben. Alle nachfolgend rekursiv stattfindenden Aufrufe der findMoves-Methode (genauer: findMovesSequential) belassen wir – der Einfachheit halber – im jeweils gestarteten Slave-Thread. In einer Verfeinerung Ihrer Implementierung wären an dieser Stelle Optimierungen der Strategie vorstellbar. Jeder Slave-Thread kann auch selbst sein eigener Master sein und so weitere Slave-Threads ins Leben rufen. Es ist also eine Hierarchiebildung im Master-Slave-Modell möglich!
Vergleichen Sie die Laufzeiten Ihres Programms bei sequentieller und paralleler Suche. Wie groß sind die Unterschiede, die Sie beobachten? Gelingt es Ihnen, die Informationen in Abbildung 2 zu erweitern?
Lösung
Quellcode: Siehe auch Github.
In Listing 1 stoßen wir auf den benutzerdefinierten Datentyp Coordinate. Mit Variablen seines Typs wird auf dem Schachbrett eine Springerposition beschrieben:
01: class Coordinate {
02:
03: friend std::ostream& operator<< (std::ostream&, const Coordinate&);
04:
05: public:
06: Coordinate() = default;
07: Coordinate(size_t row, size_t col) : m_row{ row }, m_col{ col } {}
08:
09: public:
10: // getter/setter
11: inline size_t getRow() const noexcept { return m_row; }
12: inline size_t getCol() const noexcept { return m_col; }
13:
14: // public interface
15: Coordinate fromOffset(size_t rowOfs, size_t colOfs) const noexcept;
16:
17: private:
18: size_t m_row{};
19: size_t m_col{};
20: };
Listing 1: Klasse Coordinate: Definition.
Wir definieren in Listing 1 die beiden Variablen m_row und m_col vom Typ size_t, da sie als Index für einen STL-Container verwendet werden. Beachten Sie in den Zeilen 11 und 12 die Verwendung des Schlüsselworts noexcept:
Sie teilen dem Übersetzer auf diese Weise mit, dass in dieser Methode keine Ausnahme eintreten kann – niemals!
Der Übersetzer benutzt diese Information, um effizienteren Maschinencode zu generieren.
Die Methode fromOffset und der Operator << sind einfach zu implementieren (Listing 2):
01: Coordinate Coordinate::fromOffset(size_t rowOfs, size_t colOfs) const noexcept {
02: return { m_row + rowOfs, m_col + colOfs };
03: }
04:
05: std::ostream& operator<< (std::ostream& os, const Coordinate& coord) {
06: os << "{" << coord.m_row << "," << coord.m_col << "}";
07: return os;
08: }
Listing 2: Klasse Coordinate: Implementierung.
Beachten Sie in Zeile 2 von Listing 2 die Anwendung der einheitlichen Initialisierung unter Weglassung des Typnamens (hier: Coordinate).
Da der Compiler diese Information während des Übersetzungsvorgangs kennt, können Objekte bei der Rückgabe aus Methoden ohne
Angabe des Typs erzeugt werden.
Damit sind wir schon beim Schachbrett angekommen. Wir betrachten nicht nur Schachbretter in der Standardgröße mit 8×8 Feldern.
Aus diesem Grund bietet es sich an, eine Klasse KnightProblemBoard als Template Klasse mit Wertparametern (non-type template parameter) für die entsprechende Anzahl der Reihen
und Spalten zu definieren. Damit kann der Übersetzer pro Berechnung eine optimale Schachbrett-Klasse generieren,
da er bereits – zumindest in unseren Anwendungsfällen – die
Anzahl der Reihen und Spalten vor dem Erzeugen des Schachbretts kennt!
Bei Gebrauch von Templates weichen wir vom üblichen C++ Entwicklungsmodell für Klassen (zwei Dateien, eine für die Schnittstelle – Header-Datei – und eine zweite
für die Realisierung der Klasse – Implementierungsdatei) ab. Wir wenden das so genannte Inclusion Model an und implementieren die Klasse KnightProblemBoard
in einer einzigen Datei, so wie es in anderen Programmiersprachen (zum Beispiel C# oder Java) auch üblich ist.
01: template <size_t ROWS, size_t COLS>
02: class KnightProblemBoard
03: {
04: private:
05: std::array<std::array<int, COLS>, ROWS> m_board;
06:
07: public:
08:
09: KnightProblemBoard() {
10: clearBoard();
11: }
12:
13: private:
14: void verifyCoordinate(const Coordinate& coord) const {
15:
16: if constexpr (RangeCheck) {
17: if (coord.getRow() >= ROWS || coord.getCol() >= COLS) {
18: throw std::range_error("verifyCoordinate failed !!! ");
19: }
20: }
21: }
22:
23: public:
24: int& at(const Coordinate& coord) {
25: verifyCoordinate(coord);
26: return m_board[coord.getRow()][coord.getCol()];
27: }
28:
29: const int& at(const Coordinate& coord) const {
30: verifyCoordinate(coord);
31: return m_board[coord.getRow()][coord.getCol()];
32: }
33:
34: void clearBoard() {
35: std::for_each(m_board.begin(), m_board.end(), [](auto& row) {
36: std::for_each(row.begin(), row.end(), [](auto& element) {
37: element = 0;
38: });
39: }
40: );
41: }
42: };
43:
44: template <size_t ROWS, size_t COLS>
45: std::ostream& operator<< (std::ostream& os, const KnightProblemBoard<ROWS, COLS>& board) {
46:
47: for (size_t row = 0; row != ROWS; ++row) {
48: for (size_t col = 0; col != COLS; ++col) {
49: Coordinate coord{ row, col };
50: int moveNumber = board.at(coord);
51: os << std::setw(4) << moveNumber << ' ';
52: }
53: os << std::endl;
54: }
55:
56: return os;
57: }
Listing 3: Klasse KnightProblemBoard.
Da wir die Anzahl der Reihen und Spalten nicht variabel gestalten, bietet sich als Datenstruktur für das Schachbrett
ein zwei-dimensionales std::array<T>-Objekt an. Die Elemente des Arrays sind vom Typ int,
sie beschreiben die Zugnummer des Springers beim Traversieren des Schachbretts.
In Zeile 16 von Listing 3 finden Sie einen if constexpr Ausdruck vor. Solche Ausdrücke treten nur in Templates auf,
die Bedingung muss zur Übersetzungszeit ausgewertet werden können. Wird der Ausdruck zu true evaluiert,
werden die Anweisungen im nachfolgenden Block übersetzt und führen folglich zu entsprechenden Anweisungen im ausführbaren Programm.
Im anderen Fall (false) ignoriert der Übersetzer einfach den Block komplett. An den if constexpr Ausdruck könnte sich auch ein else-Block anschließen,
der nach denselben Regeln vom Übersetzer behandelt wird.
Kurz und bündig formuliert können wir einen if constexpr-Ausdruck als compile-time if bezeichnen.
Im vorliegenden Beispiel soll es zur Übersetzungszeit möglich sein, die Methode verifyCoordinate mit oder ohne Implementierung auszustatten.
Die Implementierung der operator<<-Methode ist bei Template Klassen nicht immer ganz trivial. Ich habe den Ansatz gewählt,
den Operator einfach als globale Funktion zu realisieren. Deshalb gibt es in der KnightProblemBoard-Klasse keine entsprechende friend-Deklaration geben,
außerdem muss die Implementierung mit der öffentlichen Schnittstelle der Klasse KnightProblemBoard zurechtkommen.
Wenn Sie Zeile 16 genau studiert haben, werden
Sie beobachten, dass die Variable RangeCheck in diesem Listing nirgendwo definiert ist.
Natürlich würde dies einen Syntaxfehler nach sich ziehen, wir finden die Variablendefinition an einer anderen zentralen Stelle im Programm vor:
01: constexpr size_t Rows = 5;
02: constexpr size_t Cols = 5;
03:
04: constexpr bool Verbose = true;
05: constexpr bool VerboseSolver = false;
06: constexpr bool RangeCheck = false;
Listing 4: Datei common.h – globale Definitionen.
Damit kommen wir auf den Solver des Springerproblems zu sprechen, also die Klasse KnightProblemSolver.
Wie die Klasse KnightProblemBoard ist auch die KnightProblemSolver-Klasse eine Template Klasse, wir finden die Realisierung in einer einzigen Datei vor. Etliche Methoden dieser Klasse wie etwa setKnightMoveAt, unsetKnightMoveAt, inRange, canMoveTo, isSolution und nextKnightMoves wurden bereits in Tabelle 5 sehr ausführlich spezifiziert, ihre Realisierung sollte nach den getroffenen Vorbereitung nicht weiter schwer sein:
001: template <size_t ROWS, size_t COLS>
002: class KnightProblemSolver
003: {
004: public:
005: using Solution = std::list<Coordinate>;
006: using ListSolutions = std::list<Solution>;
007:
008: private:
009: KnightProblemBoard<ROWS, COLS> m_board; // chess board
010: Solution m_current; // solution being in construction
011: ListSolutions m_solutions; // list of found solutions
012: int m_moveNumber; // number of last knight's move
013:
014: public:
015: // c'tor
016: KnightProblemSolver() : m_moveNumber{ 0 } {}
017:
018: public:
019: // getter/setter
020: size_t getHeight() const noexcept { return ROWS; }
021: size_t getWidth() const noexcept { return COLS; }
022:
023: ListSolutions getSolutions() const {
024: return m_solutions;
025: }
026:
027: void clearSolutions() {
028: m_solutions.clear();
029: }
030:
031: // public interface
032: int findMovesSequential() {
033:
034: // reset data structures
035: m_board.clearBoard();
036: m_solutions.clear();
037: m_current.clear();
038: m_moveNumber = 0;
039:
040: // start at lower left corner
041: Coordinate start{ ROWS - 1, 0 };
042: findMovesSequential(start);
043: return static_cast<int> (m_solutions.size());
044: }
045:
046: // find all solutions using thread pool (0 == seq, >= 1 par)
047: int findMovesParallel(int maxDepth = 1) {
048:
049: // reset data structures
050: m_board.clearBoard();
051: m_solutions.clear();
052: m_current.clear();
053: m_moveNumber = 0;
054:
055: // start at lower left corner
056: Coordinate start{ ROWS - 1, 0 };
057: findMovesParallel(start, maxDepth);
058: return static_cast<int> (m_solutions.size());
059: }
060:
061: int countSolutions() {
062: return static_cast<int> (m_solutions.size());
063: }
064:
065: // functor notation needed for std::async
066: ListSolutions operator()(const Coordinate coord, int maxDepth) {
067: int count = findMovesParallel(coord, maxDepth);
068: return m_solutions;
069: }
070:
071: private:
072: // private helper - algorithm to solve the Knight's Tour problem sequentially
073: int findMovesSequential(const Coordinate& coord) {
074:
075: setKnightMoveAt(coord);
076: m_current.push_back(coord);
077:
078: if (isSolution()) {
079: // add found solution to the list of all solutions
080: m_solutions.push_back(m_current);
081: }
082: else {
083: // determine list of possible next moves
084: std::vector<Coordinate> nextMoves = nextKnightMoves(coord);
085:
086: // do next moves sequential
087: for (const Coordinate& move : nextMoves) {
088: findMovesSequential(move);
089: }
090: }
091:
092: unsetKnightMoveAt(coord);
093: m_current.pop_back();
094:
095: return static_cast<int> (m_solutions.size());
096: }
097:
098: // private helper - algorithm to solve the Knight's Tour problem in parallel
099: int findMovesParallel(const Coordinate& coord, int maxDepth) {
100:
101: setKnightMoveAt(coord);
102: m_current.push_back(coord);
103:
104: // determine list of possible next moves
105: std::vector<Coordinate> nextMoves = nextKnightMoves(coord);
106: std::deque<std::future<ListSolutions>> futures;
107:
108: int count{};
109: for (const Coordinate& move : nextMoves) {
110:
111: KnightProblemSolver slaveSolver = *this; // make a copy of the solver including the current board
112: slaveSolver.clearSolutions(); // don't reuse solutions of current solver
113:
114: if (maxDepth > 0) {
115: // do next moves parallel or ...
116: std::future<ListSolutions> future = std::async(
117: std::launch::async,
118: std::move(slaveSolver),
119: move,
120: maxDepth - 1);
121:
122: futures.push_back(std::move(future));
123: }
124: else {
125: // ... do next moves sequential
126: slaveSolver.findMovesSequential(move);
127: count += slaveSolver.countSolutions();
128:
129: // need to copy all found solutions from slave solver to current solver
130: ListSolutions solutions = slaveSolver.getSolutions();
131: if (solutions.size() != 0) {
132: m_solutions.insert(
133: std::end(m_solutions),
134: std::begin(solutions),
135: std::end(solutions)
136: );
137: }
138: }
139: }
140:
141: // block async tasks, if any, and compute final result
142: // (just use 'std::future' references to access non-copyable objects)
143: for (std::future<ListSolutions>& future : futures) {
144:
145: ListSolutions partialSolutions = future.get();
146: if (partialSolutions.size() != 0) {
147: m_solutions.insert(
148: std::end(m_solutions),
149: std::begin(partialSolutions),
150: std::end(partialSolutions)
151: );
152: count += static_cast<int> (partialSolutions.size());
153: }
154: }
155:
156: unsetKnightMoveAt(coord);
157: m_current.pop_back();
158:
159: return static_cast<int> (m_solutions.size());
160: }
161:
162: // occupy square on the chess board
163: void setKnightMoveAt(const Coordinate& coord) {
164: m_moveNumber++;
165: m_board.at(coord) = m_moveNumber;
166: }
167:
168: // release square on the chess board
169: void unsetKnightMoveAt(const Coordinate& coord) {
170: m_moveNumber--;
171: m_board.at(coord) = 0;
172: }
173:
174: // compute list of next possible moves
175: std::vector<Coordinate> nextKnightMoves(const Coordinate& coord) {
176: std::vector<Coordinate> list;
177:
178: if (Coordinate tmp{ coord.fromOffset(2, 1) }; canMoveTo(tmp))
179: {
180: list.push_back(tmp);
181: }
182: if (Coordinate tmp{ coord.fromOffset(1, 2) }; canMoveTo(tmp))
183: {
184: list.push_back(tmp);
185: }
186: if (Coordinate tmp{ coord.fromOffset(-2, 1) }; canMoveTo(tmp))
187: {
188: list.push_back(tmp);
189: }
190: if (Coordinate tmp{ coord.fromOffset(-1, 2) }; canMoveTo(tmp))
191: {
192: list.push_back(tmp);
193: }
194: if (Coordinate tmp{ coord.fromOffset(2, -1) }; canMoveTo(tmp))
195: {
196: list.push_back(tmp);
197: }
198: if (Coordinate tmp{ coord.fromOffset(1, -2) }; canMoveTo(tmp))
199: {
200: list.push_back(tmp);
201: }
202: if (Coordinate tmp{ coord.fromOffset(-2, -1) }; canMoveTo(tmp))
203: {
204: list.push_back(tmp);
205: }
206: if (Coordinate tmp{ coord.fromOffset(-1, -2) }; canMoveTo(tmp))
207: {
208: list.push_back(tmp);
209: }
210:
211: return list;
212: }
213:
214: // checks, whether coordinate does exist on the chess board
215: bool inRange(const Coordinate& coord) {
216: return
217: (coord.getRow() >= 0) && (coord.getRow() < ROWS) &&
218: (coord.getCol() >= 0) && (coord.getCol() < COLS);
219: }
220:
221: // checks, whether coordinate is valid and is still not taken
222: bool canMoveTo(const Coordinate& coord) {
223: return inRange(coord) && (m_board.at(coord) <= 0);
224: }
225:
226: // verifies, whether current list of moves is a solution
227: bool isSolution() {
228: return m_moveNumber >= ROWS * COLS;
229: }
230: };
Listing 5: Klasse KnightProblemSolver.
Die beiden öffentlichen Methoden findMovesSequential und findMovesParallel (Zeilen 32 ff. bzw. 47 ff. in Listing 5)
besitzen beide eine private Überladung, in der die eigentliche Hauptarbeit erledigt wird (Zeilen 73 ff. und 99 ff.).
Beginnen wir zunächst mit der sequentiellen Betrachtung des Springerproblems: Methode findMovesSequential setzt den Springer auf das Schachbrett (Zeile 75)
und speichert diese Koordinate auch als potentiellen Kandidaten in einem Lösungspfad ab (Zeile 76).
Die wichtigste Methode für den Algorithmus ist die kleine Hilfsmethode isSolution: Sie schaut auf dem Schachbrett nach,
ob es noch freie Felder gibt oder nicht (Zeile 78).
Wenn ja, werden ausgehend von der aktuellen Position des Springers alle möglichen Nachfolgepositionen berechnet (Zeile 84).
Diese Liste wird nun der Reihe nach durchlaufen, um von allen möglichen Nachfolgepositionen ausgehend zu berechnen,
ob sich eine Lösung des Springerproblems finden lässt: Die findMovesSequential-Methode wird zu diesem Zweck
mit allen möglichen Nachfolgeposition rekursiv aufgerufen (Zeile 88).
Am Ende der Methode wird der Springer von der aktuellen Position entfernt und auch aus dem potentiellen Lösungspfad wieder ausgetragen.
Hat ein Aufruf von isSolution ergeben, dass auf dem Schachbrett alle Felder belegt sind, haben wir eine Lösung gefunden.
Der Lösungspfad (Instanzvariable m_current) wird in eine separate Liste m_solutions umkopiert.
Eigentlich hätten wir nun mit der Methode findMovesSequential das Springerproblem bereits gelöst.
Sie werden bei der Erörterung der Vorgehensweise möglicherweise bemerkt haben, dass das Durchlaufen mehrerer Nachfolgepositionen von einer festen Springerposition aus betrachtet einen Ansatzpunkt bietet, um hier parallel vorzugehen. Genau diese Idee steckt im Entwurf der Methode findMovesParallel.
Sie ermittelt, wiederum ausgehend von einer aktuellen Springerposition, eine Liste aller möglichen Folgezüge
(Zeile 105), das Ergebnis liegt dann in einem std::vector<Coordinate>-Objekt vor.
Natürlich müssen bei einer Parallelisierung des Algorithmus die jeweiligen Tasks (Threads) ihr eigenes Schachbrett zur Verfügung haben.
Dies habe ich dadurch gelöst, dass der Einfachheit halber die jeweils beteiligten KnightProblemSolver-Objekte kopiert werden (Zeile 111).
Nun kommt die std::async-Methode ins Spiel. Sie besitzt im Wesentlichen drei Überladungen:
std::asyncmit normaler C-Funktion,std::asyncmit Funktor-Objekt undstd::asyncmit Lambda-Funktion.
Ein Aufruf mit einer normalen C-Funktion (keine Objekt-Orientierung) oder mit einer Lambda-Funktion (in diesem Anwendungsfall zu unübersichtlich) kam für mich nicht in Frage. Damit bleibt nur die Variante mit einem Funktor-Objekt übrig. Die entsprechende Realisierung des Operators operator()
finden Sie in den Zeilen 66 bis 69 vor. Im Prinzip dient der Einsatz des ()-Operators nur einem einzigen Zweck, nämlich die findMovesParallel-Methode an std::async als Parameter übergeben zu können, also eine objekt-orientierte Vorgehensweise zu haben.
Die Implementierung des ()-Operators zieht noch eine zweite Konsequenz nach sich: Es kommt zu einem
rekursiver Aufruf der findMovesParallel-Methode! Wozu ist dieser rekursive Aufruf überhaupt notwendig? Ich wollte die Parallelisierung des Algorithmus nicht nur auf eine „Ebene” beschränken (Zug von der aktuellen Position zu einer möglichen Nachfolgeposition),
sondern auch „Züge von einer Nachfolgeposition zu den Nach-Nachfolgepositionen” mit in die Parallelisierung mit einbeziehen können,
sofern dies erwünscht ist. Aus diesem Grund besitzt die
findMovesParallel-Methode einen Parameter maxDepth, der die Tiefe des rekursiven Abstiegs kontrolliert.
Ist maxDepth größer als 0, dann wird, wiederum mit einem Aufruf von findMovesParallel
(aus technischen Gründen: mit Hilfe eines entsprechenden Funktor-Objekts) eine Aufteilung der unterschiedlichen Berechnungen auf weitere Threads vorgenommen
(Zeile 116 bis 120). Andernfalls geht es in Zeile 126 mit findMovesSequential sequentiell weiter.
In Zeile 116 ist ein weiteres technisches Detail beim Aufruf von std::async zu beachten. Das Objekt, das den ()-Operator implementiert,
kann (sinnvollweise) nicht als Referenz oder Kopie an std::async übergeben werden. Es muss (mittels std::move) die Verschiebesemantik angewendet werden.
Dasselbe gilt für std::future<ListSolutions>-Objekte, die vorübergehend in einem std::deque<std::future<ListSolutions>>-Objekte abgelegt werden.
Auch hier muss die Verschiebesemantik zum Einsatz kommen.
Der Einsatz von std::async-Methoden bringt es mit sich, dass die Resultate über ein entsprechendes std::future<T>-Objekt „in der nahen Zukunft”
abgeholt werden können. Die durch std::async angestoßenen Threads stehen konzeptionell für die Slaves.
Ab den Zeilen 145 werden mit einem get-Aufruf an den jeweiligen std::future<T>-Objekten die von ihnen berechneten (Zwischen-)Resultate abgeholt und
in einen entsprechenden Container des Masters umkopiert. Da alle beteiligten Threads auf einer Kopie eines KnightProblemSolver-Objekts arbeiten,
sind während der parallelen Ausführung keine besonderen Schutzmechanismen notwendig
(die Beachtung eines etwaigen konkurrierenden Zugriffs auf gemeinsame Daten ist nicht erforderlich).
Ist ein Slave fertig, können seine Resultate im Master direkt umkopiert werden, es wird jetzt nicht mehr parallel gearbeitet.
Noch ein abschließender Hinweis: In den Zeilen 178 ff. finden Sie eine C++ 17 Spracherweiterung vor, eine if-Anweisung mit einer Variablen-Initialisierung. So ist die Variable tmp von Zeile 178 genau bis zur Zeile 181 gültig bzw. bekannt. Ihre Definition ist „innerhalb” der if-Anweisung erfolgt,
damit erklärt sich ihr minimaler Gültigkeitsbereich:
if (Coordinate tmp{ coord.fromOffset(2, 1) }; canMoveTo(tmp))
{
list.push_back(tmp);
}
Ausführung des Programms
Die Hauptarbeit in der Implementierung der Klasse KnightProblemSolver lag mit Sicherheit in der Parallelisierung des Algorithmus.
Mit den folgenden Testszenarien hoffe ich an Hand der Zeitmessungen nachweisen zu können, dass der Aufwand auch seine Mühe wert war.
Zum Vergleichen der Laufzeiten der Realisierung ziehen wir ein Schachbrett der Größe 4×7 zu Rate. Auf meinem Intel-Rechner mit einem Intel® Core™ i9-9880H CPU @ 2.30 GHz Prozessor, laut Beschreibung einer 8-Kern CPU, erhalte ich das Ergebnis
[12180]: Main: findMovesSequential():
[12180]: Elapsed time = 1220 [msecs]
[12180]: Found: 1682
[12180]: Main: findMovesParallel():
[12180]: Elapsed time = 728 [msecs]
[12180]: Found: 1682
Zum Vergleich können wir den Grad der Parallelisierung noch eine Ebene tiefer ziehen, die Ergebnisse werden noch besser:
[13008]: Main: findMovesSequential():
[13008]: Elapsed time = 1207 [msecs]
[13008]: Found: 1682
[13008]: Main: findMovesParallel():
[13008]: Elapsed time = 349 [msecs]
[13008]: Found: 1682
Man sieht, dass sich die Mühen der Parallelisierung des Algorithmus gelohnt haben!